Particiones
Dado un número natural N , ¿de cuantas
maneras diferentes podemos expresarlo como suma de otros naturales?
El primer paso a hacer es clarificar el problema. Diremos
que dos expresiones de N como
suma de naturales son la misma si permutando los números
que aparecen en la suma podemos pasar de una a la otra. Así
Una expresion de este tipo la llamaremos una partición de N. Llamaremos p(N) el número de
particiones de N. Tenemos que:
| p(n) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| n | 3 | 5 | 7 | 11 | 15 | 22 | 30 | 42 | 56 | 77 | 101 | 135 | 176 | 231 | 297 | 385 | 490 | 627 | 792 | 1002 | 1255 | 1575 | 1958 |
Aquí tenemos una lista de todas las particiones de 6:
6, 5+1, 4+1+1, 4+2, 3+1+1+1, 3+2+1, 3+3, 2+1+1+1+1, 2+2+1+1, 2+2+2, 1+1+1+1+1+1.
La función p(N) crece de forma muy rápida. Por ejemplo tenemos que (¡ejercicio!)
p(1000)=24.061.467.864.032.622.473.692.149.727.991
En esta página de Dario Alpern hay un applet de java que permite calcular las particiones de un número.
La primera pregunta que nos podemos hacer es: ¿Hay alguna fórmula para p(n)?
La respuesta a esta pregunta depende de que es lo que
entendemos por "fórmula".
Por ejemplo, la fórmula más famosa (desde
mi punto de vista) para las particiones de n se debe a Euler
, y dice:
|
1 (1-x)(1-x2)(1-x3)... |
Dicho de otra forma: si tomamos el producto infinito
| 1
1
1 (1-x) (1-x |
entonces este producto esta bien definido para los numeros reales "cerca del 0" (de hecho para los números reales con valor absoluto menor que 1) y su serie de Taylor alrededor del 0 es la serie con coeficientes p(n).
Comentario: Si tenemos una función
f(n) definida para los números naturales n, la función F(x)
definida por la suma infinita F(X):=f(0)+f(1)x+f(2)x![]() +f(3)x
+f(3)x![]() +..... se le llama la función generatriz de f(n). Aunque parezca
estraño, a veces es más facil estudiar la funcion generatriz
F que la propia función f, y deducir propiedades de f a partir de
propiedades de la función F.
+..... se le llama la función generatriz de f(n). Aunque parezca
estraño, a veces es más facil estudiar la funcion generatriz
F que la propia función f, y deducir propiedades de f a partir de
propiedades de la función F.
¿Cómo se demuestra la validez de esta
fórmula? Observemos primero que
| 1
(1-x) |
de donde, sustituyendo x por x![]() en la fórmula anterior, obtenemos una fórmula para cada
uno de los miembros del producto infinito anterior. Ahora ya solo tenemos
que multiplicar todas estas sumas infinitas para obtener la fórmula
buscada, observando que para obtener el coeficiente de x
en la fórmula anterior, obtenemos una fórmula para cada
uno de los miembros del producto infinito anterior. Ahora ya solo tenemos
que multiplicar todas estas sumas infinitas para obtener la fórmula
buscada, observando que para obtener el coeficiente de x![]() solo tenemos que multiplicar las n primeras sumas infinitas, y solo hasta
el grado n. De hecho esta "demostración" no tiene en cuenta los
problemas de convergencia de la función, problema que dejamos como
ejercicio para los más rigurosos....
solo tenemos que multiplicar las n primeras sumas infinitas, y solo hasta
el grado n. De hecho esta "demostración" no tiene en cuenta los
problemas de convergencia de la función, problema que dejamos como
ejercicio para los más rigurosos....
Claro que esta fórmula no es realmente muy útil si lo que uno quiere es calcular p(n) de una forma rápida y eficinte (por ejemplo con el ordenador).
Podemos dar alguna fórmula que se adapta un poco mejor al cálculo de p(n), suponiendo conocido p(m) para todo (o para algunos) m menor que n.
Por ejemplo:
| p(n)= |
donde la suma ![]() esta evaluada en todos los números
enteros k tales que k(3k+1)/2 y k(3k-1)/2 estan entre 1 y n,
y (-1)^(k+1) es 1 si k es impar y -1 si k es par. O sea que
esta evaluada en todos los números
enteros k tales que k(3k+1)/2 y k(3k-1)/2 estan entre 1 y n,
y (-1)^(k+1) es 1 si k es impar y -1 si k es par. O sea que
| p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+p(n-12)+p(n-15)-.......... |
Otra fórmula que nos relaciona p(n) con la suma
s(k) de todos los divisores de n (usualmente denotada sigma(k)) es la siguiente
|
1 n p(n) = n k=1 |
donde p(0)=1 (si se quiere por definición).
Para calcular s(k) observese que si k tiene como factorización en primos k=(p1a1)(p2a2)...(p2at) entonces la suma de los divisores de k es
donde
t pj(aj+1) - 1
s(k) =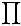

j=1 pj - 1
Finalmente podemos dar fórmulas asintóticas para p(n), o sea fórmulas que nos dan p(n) aproximadamente, y cuya aproximación es más buena como más grande sea n. La siguiente fórmula fue conjeturada por Hardy y Ramanujan y probada por Rademacher en 1937. Dice que
donde e es el número e (=2.718183...),
e 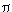
(2n/3)
p(n) ~=
4n3
Dos funciones f(x) y g(x) son asintoticamente iguales (f~=g) si el limite cuando x tiende a infinito de f(x)/g(x) es 1.Una fórmula más fácil de demostrar y que nos da a veces una estimación bastante buena (aunque peor que la fórmula de Rademacher) es
p(n) < e 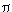
(2n/3)
Finalmente tenemos las conjeturas de Ramanujan (probadas
de hace ya tiempo)
Volver al inicio
El número p(5m+4) es divisible por 5 para todo m.
El número p(7m+5) es divisible por 7 para todo m.
El número p(11m+6) es divisible por 11 para todo m.