Uno de los muchos resultados que nos legó Pierre de Fermat ha pasado a la historia como el Pequeño Teorema de Fermat (para diferenciarlo del llamado "Ultimo Teorema de Fermat") y es un resultado  imprescindible tanto para demostrar muchos resultados de divisibilidad de números como para poder hacer según que cálculos.

El resultado en su enunciado más simple dice que

Para todo número primo p y para todo número natural n, p divide a n^p-n.

Enunciado usando congruencias, nos dice que

Para todo número primo p y para todo número natural n,  n^p=n (mod p).

O, de forma equivalente,

Para todo número primo p y para todo número natural n no divisible por p,  n^p-1= 1 (mod p).

Vamos a dar dos demostraciones de este resultado; en la segunda probaremos un resultado más general llamado el teorema de Fermat-Euler.

Primera demostración

Demostraremos el resultado en su primera formulación por inducción. Para demostrarlo necesitaremos el Binomio de Newton y los números combinatorios

Consideremos primero el caso n=1. Tenemos que 1^p-1=0, que es claramente divisible por p.

Vamos ha hacer el caso n=2, dado que ya contiene la parte más importante de la demostración.

Usando el Binomio de Newton tenemos que

			p
2p	= (1+1)p	=		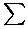(	p	)
					m
			m=0

Los sumandos primero y último son los dos iguales a 1. Así tenemos que

		p-1
2p -2	=		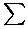(	p	)
				m
		m=1

Vamos a demostrar que todos los sumandos de esta suma son divisibles por p.

Recordemos que

(	p	)	=	p!
	m			m!(p-m)!

Dado que p divide claramente el numerador, pero no divide al denominador (ya que tanto m  como p-m son menores que p por hipótesis), este número entero es divisible por p.

Vamos a demostrar ahora el caso general. Supongamos que sabemos nuestro resultado para un n dado, y vamos a demostrar que entonces es cierto para n+1. Aplicando el binomio de Newton tenemos que

			p
(n +1)p		=		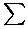(	p	)	nm·1p-m
					m
			m=0

Como ya hemos dicho antes, los dos números combinatorios en los extremos valen 1, por lo tanto

				p-1
(n + 1)p - (n + 1)		=	np-n+		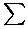(	p	)	nm
						m
				m=1

El primer sumando es divisible por p por inducción, y los números combinatorios que aparecen en el segundo sumando son todos divisibles por p, por lo tanto la resta (n +1)^p - (n+1) es divisible por p.

Segunda demostración

Vamos a demostrar el llamado teorema de Fermat-Euler:

Teorema (Fermat-Euler)  Si  n>0 es un número natural, sea f(n) es la cantidad de números naturales entre 0 y n que son primos con n:

f(n):={ 0<a<n   |   a es primo con n }. Entonces para todo número entero a primo con m se tiene que a^f(n)=1 (mod n).

Por ejemplo tenemos que si p es un número primo f(p)=p-1, ya que todos los números entre 1 y p-1 son primos con p.

Para demostrar esto empecemos por observar que el conjunto de restos modulo m invertibles por la multiplicación tiene f(n) elementos.

Proposición: El conjunto de elementos de Z/nZ que tienen inverso por la multiplicación corresponde exactamente al conjunto de clases de congruencia de números que son primos con n.

Este resultado se deduce de la llamada identidad de Bezout: Dados dos números naturales n y m, coprimos entre si, existen dos números enteros a y b tales que

a · n + b · m = 1

Esta identidad se demuestra fácilmente usando por ejemplo el algoritmo de Euclides: se trata de hacer la división entera de n entre m (supongamos por ejemplos que n>m), e ir repitiendo esta división ahora entre m y el resto obtenido anteriormente, hasta llegar a resto 1. Esto es posible exactamente si los números n y m son coprimos entre si. Volviendo para atrás los pasos dados obtenemos la identidad de Bezout buscada.

Vamos a hacerlo con un ejemplo concreto: Tomemos n=30 y m=13. Entonces

30=13·2+4
13=4·3+1

Por lo tanto

1=13 + 4·(-3)=13+ (30+13·(-2))·(-3)=(-3)·30+7·13

De la identidad de Bezout a · n + b · m = 1 obtenemos, al hacer módulo n, que b · m =1 (mod n), y por lo tanto que m tiene inverso módulo n igual a b.

Por ejemplo, el inverso de 13 módulo 30 es igual a 7.

Observemos ahora que el conjunto G de elementos invertibles módulo m forma un grupo abeliano respecto la multiplicación: o sea que tenemos una operación, la multiplicación, de forma que se cumplen las siguientes propiedades: 

• Asociativa: Para todos a, b y c de G, (a·b)·c=a·(b·c).
• Existencia de elemento neutro: Existe un elemento de G, el 1, tal que a·1=1·a=a para todo a en G.
• Existencia de inverso: Para todo a en G, existe un elemento b en G tal que a·b=b·a=1.
• Conmutativa: para todo a y b en G se tiene que a·b=b·a.
  

Para nuestro grupo G, tenemos que tiene un número finito de elementos igual a f(n) por la proposición anterior. El teorema de Fermat-Euler se deduce entonces del siguiente resultado elemental de grupos abelianos finitos:
Lema:
Sea G un grupo abeliano finito y sea r su número de elementos. Entonces, para todo elemento a de G se tiene que a^r= 1.

Demostración:
Sea a un elemento de G. Observemos que si b y c son elementos de G diferentes, entonces a·b  y a·c son también diferentes; esto se deduce de la tercera propiedad de grupo, ya que si a·b=a·c, multiplicando por el inverso a^-1 de a a los dos lados, tenemos b=a^-1·a·b=a^-1·a·c=c, en contradicción con la hipótesis que b y c son diferentes.
Tenemos por lo tanto que los conjuntos G y a·G:={a·b: b en G} son iguales. Así, si  G={b₁,b₂,...,b_r}, se cumple la siguiente igualdad:

b₁·b₂····b_r = a·b₁·a·b₂····a·b_r = a^r·b₁·b₂····b_r

Dado que b₁·b₂····b_r  es un elemento de G, tiene inverso, y multiplicando en la igualdad anterior por su inverso obtenemos que 1= a^r como queríamos demostrar.
 

Remarquemos finalmente que este lema es cierto si G es un grupo finito no necesariamente
abeliano (o sea que no cumple la propiedad commutativa para todos los a y b en G). Su demostración es fácil usando el llamado Teorema de Lagrange que podeis encontrar en cualquier libro de Álgebra básica.