El postulado de Bertrand
Para todo número natural n , siempre
existe un número primo p mayor que n
y menor que 2n
Los números primos son los componentes fundamentales
de todos los números enteros, así como los
átomos lo son de la materia. De este modo, el estudio de los
números primos es fundamental para entender a fondo las propiedades
de los números naturales. Recordemos que un número p
es primo si sus únicos divisores son él mismo y 1. Se
tiene que todo número natural se expresa como producto de números
primos (de forma única salvo permutaciones).
La pregunta más básica que podemos hacernos
sobre los números primos es: ¿cuantos números
primos hay?
Una primera respuesta a la pregunta podría ser:
hay infinitos.
En efecto, tal como nos explico Euclides ya hace muchos
siglos, si tenemos un número n finito de primos, digamos p1,p2,p3,... ,pn ,entonces N=p1.p2.p3...pn+1 no es divisible por ninguno de ellos (¿por que?), con
lo cual existe algún otro primo.
Por cierto que de este argumento deducimos que, si denotamos
por pn el enésimo número
primo por orden creciente (p1=2,
p2=3, p3=5,...), entonces para algún m>n, pm divide a p1.p2.p3...pn+1, de donde se deduce por inducción que pn<2n (Ejercicio!). Este es
un primer resultado sobre cual es el tamaño del primo enésimo.
Otra posible respuesta podría ser responder a
la pregunta: ¿cuantos números primos hay menores
que un número dado?
Esto es lo que nos dice el teorema fundamental
de los números primos: el número de primos menores
o iguales que x es asintóticamente igual a x/log(x).
Este resultado, conjeturado por A.M.Legendre
y C.F.
Gauss, fue demostrado por J.
Hadamard y (de forma independiente) por C.
de la Vallée Poussin en 1896 utilizando métodos de
análisis complejo. En 1949 P.
Ërdos y A.
Selberg encontraron una demostración que usa "solo" resultados
de teoría de números y un poco de análisis real.
De este resultado se deduce que pn es aproximadamente igual a n·log(n) si n es muy grande.
Para ver un comentario sobre este resultado mirar
aquí
(en castellano) o bien aquí
(en ingles y mucho más completo).
Aun otra posibilidad seria preguntarnos como están
distribuidos los números primos dentro de los números
reales. Por ejemplo: si damos dos números naturales
n y m, ¿cuando podemos asegurar que existe un número primo
entre ellos dos?
Una primera respuesta a este problema nos la da el postulado
de Bertrand: En 1845 el matemático francés Joseph
Bertrand verificó que para cada entero n entre 2 y 6,000,000
existe siempre como mínimo un primo entre n y 2n.
Este resultado pero para todo número n fue demostrado
por primera vez por el matemático ruso P.L.
Chebychev en 1851.
Vamos a dar una demostración "elemental" de este
postulado, o sea una demostración donde se usan solo resultados
"elementales" de matemáticas. Esta demostración es debida
a P.
Ërdos, uno de los matemáticos mas geniales de este
siglo, que la descubrió cuando tenia solo 18 años.
Necesitaremos primero recordar algunos resultados sobre
números combinatorios.
Números combinatorios
Ahora ya estamos preparados para ver la demostración
del postulado de Bertrand:
| El postulado de Bertrand (llamado también
el teorema de Chebichev):
Para todo número natural n>1
siempre existe un número primo p mayor que n y menor que 2n.
|
La demostración se divide en varias partes, y
se basa en un estudio bastante delicado de algunos números combinatorios.
Usaremos la letra p para denotar a un número primo. Dado un
número natural n y un número primo p, la máxima
potencia de p que divide a n la llamaremos la valoración p-ádica
de n y la denotaremos vp(n).
Vamos a considerar el coeficiente binomial
C(2m+1,m) , que llamaremos M, o sea
| M=C(2m+1,m)=( |
2m+1 |
) |
= |
(2m+1)! |
| m |
m!(m+1)! |
Sea p un número primo tal que m+1 < p <=
2m+1. Entonces p divide al numerador de M pero no al denominador, por
lo tanto p divide a M. Por lo tanto el producto de todos estos primos
divide a M, y tenemos que
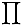
|
p |
<= |
M |
| m+1<p<=2m+1 |
|
|
|
Por otra parte, la expansión binomial de (1 +
1)2m+1 tiene dos términos iguales
a M, C(2m+1,m) y C(2m+1,m), así 2M <22m+1 y por lo tanto M < 22m,
de donde tenemos
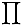
|
p |
< |
22m |
| m+1<p<=2m+1 |
|
|
|
Por reducción al absurdo. Supongamos que
exista un número n tal que no hay ningún número
primo mayor que n y menor que 2n. Consideremos el número
| N=C(2n,n)=( |
2n |
) |
= |
(2n)! |
| n |
(n!)2 |
Los números primos mayores que n y menores
que 2n dividen el numerador pero no el denominador, por lo tanto dividen
a N. Dado que por hipótesis no hay tales primos, ningún
primo mayor que n divide a N.
Vamos a demostrar que de hecho ningún primo mayor
que (2/3)n divide a N (este es, según Ërdos, el punto clave
de la demostración).
Efectivamente, supongamos que tenemos p>2 un
número primo cumpliendo que
2n/3 < p < n
Entonces, multiplicando por 2 tenemos que
n < 4n/3 < 2p < 2n
y multiplicando por 3 tenemos que
2n=6n/3 < 3p
Por lo tanto p divide a n! y p2
no divide a n!, mientras que p2 divide a (2n)! y p3 no
divide a (2n)!. Así que la valoración p-ádica de
(n!)2 y de (2n)! es la misma, de donde
p no divide a N.
(Obsérvese que la condición p>2
es cierta si n>4, cosa que supondremos a partir de ahora ya que hasta
n=4 si que se cumple el postulado de Bertrand).
Vamos a dar una acotación para la valoración
p-ádica de N, vp(N), válida
para todo primo p. Tenemos que
| vp(N)=vp((2n)!)-2vp(n!) |
= |
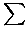
|
([2n/pr]-2[n/pr]) |
|
|
r>0 |
|
usando la fórmula que encontramos en la
sección de números combinatorios.
Observemos que para todo número real x
se tiene que [2x]-2[x] es igual a 0 o a 1 (dependiendo de si la parte
fraccionaria de x es menor o mayor que 0.5), por lo tanto
vp(N) es igual
al número de sumandos no cero del sumatorio. Dado que si pr>2n entonces
tanto [2n/pr]
como [n/pr] valen 0, tenemos que como
mucho hay log(2n)/log(p) sumandos.
Como el número de sumandos es un número
entero (evidentemente!), obtenemos
válida para todo primo p.
El siguiente paso de la demostración es ver que
Si p> 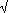 (2n), entonces vp(N)
= 0 o vp(N) = 1.
Efectivamente, si p>
(2n), entonces vp(N)
= 0 o vp(N) = 1.
Efectivamente, si p> 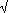 (2n), entonces log(p)>log(2n)/2, y por lo tanto
log(2n)/log(p)<2.
(2n), entonces log(p)>log(2n)/2, y por lo tanto
log(2n)/log(p)<2.
De la fórmula anterior tenemos que
| vp(N) |
< |
[log(2n)/log(p)]<2 |
Por otra parte, usando la misma fórmula podemos
encontrar una acotación para pv
si v denota a vp(N). En efecto
pv < plog(2n)/log(p) = 2n
por la definición del logaritmo (usar por
ejemplo que log(2n)/log(p)=logp(2n) donde
logp es el logaritmo en base p).
Bueno, respiremos un momento antes de subir la
última cuesta que nos llevará a la cima.
Vamos a dividir N como el producto de los primos hasta 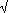 (2n) y los primos de
(2n) y los primos de 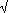 (2n) hasta
(2n) hasta
(2/3)n. Sabemos que no hay más por hipótesis.
| N= |
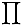
|
pvp |
= |
( |
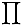
|
pvp |
) |
( |
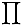
|
pvp |
) |
< |
( |
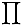
|
2n |
) |
( |
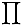
|
p |
) |
< |
(2n)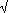 (2n)·2(4/3)n
(2n)·2(4/3)n |
|
p<=2n |
|
|
|
p<=
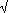 (2n)
(2n) |
|
|
|
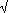 (2n)<p<=(2/3)n
(2n)<p<=(2/3)n |
|
|
|
|
p<=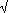 (2n)
(2n) |
|
|
|
p<=(2/3)n |
|
|
|
|
Usamos el símbolo vp para denotar la valoración
p-ádica de N, y hemos usado todos los resultados anteriores.
Por otra parte sabemos por el tercer paso que
22n /(2n) <
N ,
de donde obtenemos que
22n /(2n) <
N <(2n)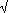 (2n)·2(4/3)n .
(2n)·2(4/3)n .
Vamos a deducir una contradicción de este hecho,
con lo cual la hipótesis inicial no será cierta. La desigualdad
anterior es equivalente a
2(2n/3)=2(2/3)n < (2n)(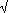 (2n) + 1).
Vamos a ver que esta desigualdad no es cierta
si n>967.
(2n) + 1).
Vamos a ver que esta desigualdad no es cierta
si n>967.
En efecto, tomando logaritmos en la desigualdad
obtenemos
(2n/3) log(2) < (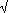 (2n) + 1) log(2n)
Llamemos x=
(2n) + 1) log(2n)
Llamemos x=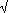 (2n). Entonces tenemos la desigualdad
(x2/3) log(2)
< (x + 1) log(x2)
y por lo tanto
x2 < (6/log(2))(x
+ 1) log(x)<(6/log(2))(2x)log(x)=(8/log(2))(x log(x))
o sea
x <(8/log(2)) log(x)
Consideremos la función
f(x)=x-(8/log(2)) log(x)
Su derivada es
(2n). Entonces tenemos la desigualdad
(x2/3) log(2)
< (x + 1) log(x2)
y por lo tanto
x2 < (6/log(2))(x
+ 1) log(x)<(6/log(2))(2x)log(x)=(8/log(2))(x log(x))
o sea
x <(8/log(2)) log(x)
Consideremos la función
f(x)=x-(8/log(2)) log(x)
Su derivada es
f'(x)=1-(8/log(2)) (1/x)
que vale cero solo cuando x=(8/log(2)), siendo
positiva si x>(8/log(2)). Por lo tanto f(x) es creciente a
partir de (8/log(2)). Dado que f(44)=.32454705>0, f(x)>0 si x>=44.
Por lo tanto
la desigualdad se cumple solo si x<44, o
sea si n < (44)2/2 = 968.
Conclusión: Si n>969, entonces existe
un número primo mayor que n y menor que 2n.
¿Y si n<=968? Entonces esta claro que se cumple
el postulado de Bertrand. Por ejemplo,
considerando los números primos:
2, 3, 5, 7, 13, 23, 43, 83, 163, 317, 521, 1039
que tienen la propiedad que cada uno es mayor
que el antecesor pero menor que su doble.
Fin de la demostración
Comentario: Este argumento se puede modificar
para dar la demostración del Teorema de J.J.Sylvester
: Para todo n>1 y para todo k menor o igual que n/2 se verifica
que existe un primo mayor que k que divide a C(n,k). (Este resultado
generaliza claramente el postulado de Bertrand).
Ejercicio Final: Demostrar (usando el postulado
de Bertrand si se quiere) que n! nunca puede ser un cuadrado.
Volver al inicio