![[Maple Metafile]](LibroMaple031_files/LibroMaple031.gif)
Ingeniería Técnica en Informática
Prácticas y problemas resueltos con Maple V
Introducción a la
PROGRAMACIÓN EN MAPLE
| > | sec1:=4,Pi,7.5,E,{1,2,3},x->3*x^2; |
Puedes acceder a sus elementos escribiendo el lugar que ocupan en la secuencia entre corchetes:
Así por ejemplo el segundo elemento de sec1 es pi.
| > | sec1[2]; |
| > | sec1[5]; |
| > | sec1[6]; |
![]() Mira ahora más detalles en la
ayuda para secuencias.
Mira ahora más detalles en la
ayuda para secuencias.
Detente sobre la ayuda o vuelve sobre ella, es importante ir entendiendo bien los conceptos.
Por ejemplo, para construir una secuencia de 10 ceros se puede escribir:
| > | 0$10; |
Para construir la secuencia de los 20 primeros números impares:
| > | seq(2*i-1,i=1..20); |
O los 10 primeros múltiplos de 3:
| > | seq(3*i,i=1..10); |
![]() Mira la ayuda para el comando
seq
.
Mira la ayuda para el comando
seq
.
| > | sec1:=4,8,13,{Pi,E,I},seq([k,k+2],k=6..18); |
(1) ¿ Qué comando te devuelve el séptimo elemento de sec1?
| > |
| > |
| > |
(2) Escribe un comando que devuelva una secuencia con once palabras `bien`.
| > |
| > |
| > |
(3) Otra manera de hacer esto es....
| > |
| > |
| > |
(4) Haz una secuencia formada por los cubos X^3 de números naturales que verifican X^3<1000.
| > |
| > |
| > | sec1:=seq(i^4,i=1..5); lista1:=[seq(i^4,i=1..5)]; |
Dada una lista, puedes acceder a la secuencia de sus elementos mediante el comando op :
| > | op(lista1); |
| > | sec2:=sec1,a,a; |
| > | lista2:=[op(lista1),muchos,mas]; |
| > | lista2[2]; nops(lista2); |
| > |
Para sustituir elementos en una lista se usa el comando subsop
| > | meses:=[enero, febrero, marzo, abril, mayo]: |
| > | subsop(2=junio,meses); |
| > | subsop(3=febrero,meses); |
Y sirve para borrar elementos de una lista, sustituyendo por NULL
| > | subsop(1=NULL,meses); |
Como en el caso de las secuencias, realiza los siguientes ejercicios sobre listas:
| > | a:=seq(i,i=1..60): |
| > | s:=2,3,4,5,t,y,j,a,a,l^2; |
(1) Determinar el número de elementos de la secuencia s :
| > |
| > |
(2) Construir la lista de los 30 primeros cuadrados (esto es, 1^2, 2^2, 3^2....)
| > |
| > |
( 3) Determinar el término que ocupa el lugar vigésimo en la lista [s].
| > |
| > |
![]() Echa una ojeada a la
ayuda para conjuntos.
Echa una ojeada a la
ayuda para conjuntos.
| > | restart; |
| > | A:={1,2,3,4,1,4,5}; |
| > | B:={1,2,1,b,s,b,c,4}; |
| > | A union B; |
| > | A intersect B; |
| > | A minus B; |
Definimos los siguientes conjuntos, listas y secuencias:
| > | s:={Luisa, Juan, Alicia, Pedro, Susana}; |
| > | t:={Pedro, Julian, Sebastian, Juan, Ana}; |
| > | lista:=[Lunes,Martes,Sabado,Jueves]; |
| > | s1:=g,e,y,d,e,r,f,y,f,d,e,k,y,e,f,g,h,d,y; |
| > |
(1) ¿Cómo puedes obtener los elementos comunes a s y t ? ¿Y los elementos de s que no están en t ?
| > |
| > |
| > |
(2) Reemplaza el elemento S abado por un nuevo elemento Miercoles en lista.
| > |
| > |
| > |
(3) ¿Cómo puedes saber cuántos elementos tiene el conjunto cuyos elementos son los de s1?
| > |
| > |
| > |
(4) Genera la lista formada por la concatenación de los elementos de lista y lista2 (definida abajo)
| > | lista2:=[elem1,elem2,elem3]; |
| > |
| > |
| > |
( 5) ¿Cuántos números menores que 1000 son a la vez el cuadrado y el cubo de un número entero?
| > |
| > |
Por otro lado están las condicionales de la forma:
si condición entonces operación1 si no operación 2
lo que significa que mientras se verifique la condición ha de realizarse la operación.
Y combinaciones de las mismas. Veremos algunos ejemplos.
Generemos un procedimiento que calcula el máximo de dos números.
Las condicionales se empiezan por if y se terminan con fi.
if condición then operación1 else operación 2 fi
Por ejemplo para calcular el máximo de dos números:
| > | maximo:=proc(a,b) local c: if (a>b) then c:=a else c:=b fi: c; end: |
La sentencia condicional es exactamente la elección del máximo.
Como c va seguida de un punto y coma, será lo que se vea en la pantalla, la asignación a la salida..
El comando end termina el procedimiento.
| > | maximo(2,4); |
Veamos un procedimiento que indica el signo de un número real:
| > | signo:=proc(a) local s; if a<0 then s:=menos elif a=0 then s:=0 else s:=mas fi: s; end: |
| > | signo(27); |
| > | signo(-23); |
| > | signo(0); |
| > |
| > |
En Maple, la forma general de un bucle es la siguiente:
for variable from inicio by salto to final while expresión do operaciones od
Si omitimos algunas de estas cláusulas, Maple les asigna un valor por defecto:
Por ejemplo para sumar los números del 1 al 10000.
| > | S:=0: for i from 1 to 10^4 do S:=S+i: od: S; |
Que coincide con el valor de la suma de los términos de una sucesión aritmética:
| > | (10^4)*(10^4+1)/2; |
Para sumar los elementos de una lista numérica:
| > | a:=[1,2,3,4,5,6,7,8]; |
| > | S:=0: for i from 1 to nops(a) do S:=S+a[i]: od: S; |
| > |
| > |
Suma de los términos de una sucesión
| > | restart; |
| > | suma:=proc(A::list) local S,i: S:=0: for i from 1 to nops(A) do S:=S+A[i]: od: S; end: |
| > | ?type; |
| > | suma(2,3,4,5,6,6); |
Error, invalid input: suma expects its 1st argument, A, to be of type list, but received 2
| > | L:=[seq(a+i*d,i=1..50)]: |
| > | suma(L); |
| > |
Generar coordenadas de un rectángulo
La primera línea de la subrutina especifica su nombre y los argumentos de entrada:
rectangulo:=proc(x,h::positive)
| > | rectangulo:=proc(x,h) [[x-.25,0],[x+.25,0],[x+.25,h],[x-.25,h]]: end; |
| > | rectangulo(-2,3); |
| > | rectangulo(0,0); |
| > |
Y se pueden representar gráficamente:
| > | with(plots): polygonplot(rectangulo(5,3)); |
Warning, the name changecoords has been redefined
| > |
| > |
| > | busqueda:=proc(a::list,b::numeric) local i,c: c:=0: for i from 1 to nops(a) while c=0 do if a[i]=b then c:=1 fi: od: if c=0 then c:=No else c:=Si fi: c; end: |
| > | busqueda([1,2,3,4,7,8],8); |
| > | busqueda([1,2,3,4,7,8],9); |
| > | busqueda([1,4,5,6,7,9,10],5); |
| > | busqueda([1,3,4,5,2,3,4,8],4); |
| > | busqueda([1,3,4,5,2,3,4,8],8); |
| > |
| > |
| > |
| > | media:=proc(a::list) local S,i: S:=0: for i from 1 to nops(a) do S:=S+a[i] od: S/nops(a); end: |
| > | media ([1,2,3,4,5,6]); |
| > |
| > |
| > |
| > | Maximo:=proc(a) local c,i: c:=a[1]: for i from 2 to nops(a) do if c<a[i] then c:=a[i] fi: od: c; end: |
| > | Maximo([44,55,6,7,10]); |
| > | Maximo([45,789,10^6,45,6]); |
Puedes probar con otros ejemplos.
| > |
| > |
- Máximo común divisor y mínimo común múltiplo
- Criptografía de clave pública
| > | with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > |
Para calcular el resto de la división de dos números enteros a,b se usa el comando mod.
| > | 5 mod 3; |
| > | 10375378 mod 124903; |
Para resolver congruencias lineales en una indeterminada, podemos usar msolve .
| > | msolve(3*y=1,7); |
De esta forma hemos resuelto la congruencia puesto que:
| > | 3*5-1 mod 7; |
Ahora resolvamos un problema similar cambiando 7 por 6:
| > | msolve(3*y=1,6); |
| > |
Parece que Maple ha fallado, pero en realidad no ha aportado ninguna solución porque no existe.
| > | seq(3*i mod 6,i=0..5); |
| > |
![]() ¿Cuál es la razón de que no tenga solución esta ecuación y sin embargo sí la tenga la anterior?
¿Cuál es la razón de que no tenga solución esta ecuación y sin embargo sí la tenga la anterior?
2.2. Máximo común divisor. Mínimo común múltiplo
Veamos algunos ejemplos de uso de la función igcd y otras funciones relacionadas:
| > | igcd(3,6); |
| > | igcd(6,4,12); |
Para calcular el máximo común divisor de todos los enteros entre 10 y 100 hacemos:
| > | igcd(seq(i,i=10..100)); |
Y debe ser 1 porque entre el 10 y el 100 hay números primos.
| > | ilcm(101,13); |
| > | ilcm(6,4,12); |
| > | ilcm(seq(i,i=10..100)); |
| > |
El comando is de la línea siguiente determina si dos expresiones son iguales.
| > | is(125*3490=ilcm(125,3490)*igcd(125,3490)); |
| > |
| > |
| > | 2*3-1*5; |
| > |
| > | igcdex(3,5,a,b); |
| > | a,b; |
| > |
| > | igcd(324,779); |
| > | igcdex(324,779,x,y); x; y; |
| > | 324*x+779*y; |
| > |
Maple se puede usar para resolver sistemas de congruencias mediante el teorema chino del resto.
Para resolver el sistema formado por las tres congruencias siguientes,
empleamos la función chrem ( ch inese rem ainder theorem) del siguiente modo:
| > | chrem([2,3,2],[3,5,7]); |
| > |
| > |
| > |
| > | with(numtheory); |
La función ifactor descompone un número entero en sus factores primos:
| > | ifactor(100); |
| > | ifactor(12345); |
| > | ifactor(39248675928359283654928364); |
| > | h:=2^33*3^55; |
| > | ifactor(h); |
| > |
| > |
| > |
| > |
| > | with(numtheory): |
| > | Testprimo1:=proc(a) local i,s,c: s:=0: for i from 2 to a-1 while s=0 do if a mod i = 0 then s:=1 fi: od: if i<a then c:=compuesto else c:=primo fi: c; end: |
| > | Testprimo1(9); |
| > | Testprimo1(17); |
| > | Testprimo1(34567890); |
| > |
| > | isprime(101); |
| > | isprime(2342138342111); |
| > | isprime(23218093249834217); |
| > |
![]() Como éste número no es muy grande, puedes comprobar factorizándolo que, en efecto, no es primo.
Como éste número no es muy grande, puedes comprobar factorizándolo que, en efecto, no es primo.
| > |
| > |
| > |
| > |
| > |
| > | ithprime(1);ithprime(2);ithprime(3); |
| > | ithprime(3000); |
| > |
| > |
| > | nextprime(1000); |
| > | prevprime(1000); |
| > | nextprime(13); |
Observa que si el número es primo nextprime te da el siguiente primo y prevprime el primo anterior.
| > | phi(1); |
| > | phi(2); |
| > | phi(10); |
| > | is(phi(13)=12); |
Esto indica que 13 es un número primo.
| > | phi(5); |
| > | phi(10); |
| > | phi(107); |
Así construimos otro test de primalidad:
| > | Testprimo2:=proc(a) local c: if is(phi(a)=a-1)=true then c:=si else c:=no fi: c; end: |
| > | Testprimo2(37); |
| > | Testprimo2(5); |
| > | Testprimo2(107); |
| > | Testprimo2(32); |
| > | invphi(2); |
| > |
Los únicos números cuyo valor de phi es 2 son el 3, el 4 y el 6.
| > | phi(3),phi(4),phi(6); |
| > |
| > | s:=invphi(6); |
| > | p:=[]: for i from 1 to nops(s) do p:=[op(p),phi(s[i])]: od: p; |
| > |
En esta sección veremos algunas aplicaciones de la aritmética modular y las congruencias.
Necesitamos convertir letras en números, para lo cual emplearemos la función letranumero.
| > | alias(I=I); alias(E=E); |
Error, use interface(imaginaryunit=...) to set the imaginary unit
| > | alfabeto:=["A","B","C","D","E","F","G","H","I","J","K","L","M","N","Ñ","O","P","Q","R","S","T","U","V","W","X","Y","Z"]: |
Y la función letranumero es, en general:
| > | letranumerogen:=proc(a::list) local i: for i from 1 to nops(a) do letranumero(a[i]):=i-1; od: end: |
| > | letranumerogen(alfabeto): letranumero("U"); |
| > |
| > | numeroletragen:=proc(a::list,b::list) local i: for i from 0 to nops(b) do numeroletra(i):=a[i+1]; od: end: |
| > | numeroletragen(alfabeto,[seq(i,i=0..nops(alfabeto)-2)]): numeroletra(21); |
| > |
Un encriptador afin clásico es de la forma:
![]() ¿Cuál es la condición para que eso ocurra, esto es, para que
f
tenga inversa?
¿Cuál es la condición para que eso ocurra, esto es, para que
f
tenga inversa?
| > | Encripletra:=proc(s::string,clave::[integer,integer]) local factor,incremento; if not length(s) = 1 then ERROR(`el argumento debe ser una sola letra`); fi; factor:=clave[1]; incremento:=clave[2]; RETURN(numeroletra((letranumero(s)*factor+incremento) mod 26)); end: |
| > |
| > | Encripta := proc(s::string, clave::[integer,integer]) local i,textocifrado; textocifrado:=NULL; for i from 1 to length(s) do textocifrado:= cat(textocifrado, Encripletra(substring(s,i..i),clave)); od; RETURN(textocifrado); end: |
| > |
| > | Encripletra("A",[3,5]); |
| > | Encripta("QUIENSABEDONDE",[3,7]); |
| > |
| > |
| > |
| > |
3.2. Criptografía de clave pública
| > | Generaclaves:=proc(p::integer,q::integer) local n, #modulo e, #exponente d, #d*e=1 (mod phin) phin; #phi(n)=(p-1)(q-1) n:=p*q; #calcula el modulo (publico) phin:=(p-1)*(q-1); e:=13; #este numero se podria generar aleatoriamente #calculamos d tal que e*d=1 (mod phin) d:=op(1,op(Roots(e*x-1) mod phin)); RETURN([[n,e],[n,d]]); end: |
| > |
| > | Generaclaves(43,59); |
Efectivamente cumplen lo que deben:
| > | is(2537=43*59); is(13*937 mod phi(2537)=1); |
Función de cifrado y descifrado
Ahora que sabemos generar claves, vamos a ver el método RSA de encriptado. El código es sencillo:
| > | RSA:=proc(key,msg::list(posint)) local ct, #texto cifrado obtenido pe, #exponente (público) pm, #modulo (público) i; #índice del bucle pm:=key[1]; pe:=key[2]; ct:=[]; for i from 1 to nops(msg) do ct:=[op(ct),msg[i]^pe mod pm]; od; RETURN(ct); end: |
Veamos cómo utilizar el sistema RSA para transmitir un mensaje:
Primero asignamos a cada letra un número de dos cifras (empezaremos por el 10 por comodidad) y al
espacio en blanco otro número para separar palabras.
| > | alias(I=I); alias(E=E); alfabeto:=["A","B","C","D","E","F","G","H","I","J","K","L","M","N","Ñ","O","P","Q","R","S","T","U","V","W","X","Y","Z"," "]: for i from 1 to nops(alfabeto) do letranumero(op(i,alfabeto)):=i+9: od: |
Error, use interface(imaginaryunit=...) to set the imaginary unit
| > |
| > | bloques:=proc(msg::string) local i,listabloques; i:=1;listabloques:=[]; while i < length(msg) do listabloques:=[op(listabloques), letranumero(substring(msg,i..i)) * 100 + letranumero(substring (msg ,i+1..i+1))]:i:=i+2: od; RETURN(listabloques); end: |
| > |
| > | bloques("HOLA QUE TAL"); |
| > | Generaclaves(83,61); |
| > |
que previamente debemos comunicarle. La forma de hacerlo es la siguiente:
| > | RSA([5063, 13],bloques("HOLA QUE TAL")); |
| > |
De esta forma, el mensaje que nos enviarán será:
![]()
y no importa que nadie lo lea, porque no serán capaces de entenderlo.
| > | RSA([5063, 757],[2780, 980, 2926, 3809, 119, 798]); |
| > |
Como vemos esta lista se corresponde con el mensaje "HOLAQUETAL":
| > | bloques("HOLA QUE TAL"); |
| > |
4. Test resuelto del curso 2000/2001
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | igcd(5643,985798); igcdex(5643,985798,a,b): a; b; |
| > |
| > |
| > |
| > | chrem([44,-8,25,0],[99,50,31,13]); |
La respuesta correcta es la b).
| > |
| > |
| > |
| > | [nextprime(10^6),nextprime(2*10^6),nextprime(3*10^6)]; |
La respuesta correcta es la c).
| > |
4. Calcula cuántos números primos hay entre 100.000 y 200.000.
| > |
| > | c:=0; for i from 10^5 to 2*10^5 do if isprime(i) then c:=c+1 fi; od; c; |
La respuesta correcta es la b).
| > |
5. Sea la función f(n)=n^17 mod 17. Señala la respuesta correcta:
| > |
| > | seq([n,n^(17) mod 17], n=0..16); |
La respuesta correcta es la a).
| > |
| > |
| > |
| > | restart; with(numtheory): c:=0; for i from 0 to 10^3 do if isprime(i^2+i+41) then c:=c+1 fi; od; evalf(100*c/1001); |
Warning, the protected name order has been redefined and unprotected
La respuesta correcta es la c).
| > |
7. Y en el conjunto {g(0),g(1),...,g(10.000)}, ¿cuál es el porcentaje de números primos?
| > |
| > | restart; with(numtheory): c:=0; for i from 0 to 10^4 do if isprime(i^2+i+41) then c:=c+1 fi; od; evalf(100*c/10001); |
Warning, the protected name order has been redefined and unprotected
La respuesta correcta es la c).
| > |
| > |
| > | (1513 mod 7, 1513 mod 13, 1513 mod 19); |
| > | (1206 mod 7, 1206 mod 13, 1206 mod 19); |
La respuesta correcta es la c).
9. La función f(p)=77p+42 (mod 98) es:
| > |
| > | {seq(77*p+42 mod 98,p=0..97)}; |
La respuesta correcta es la c).
| > |
| > | invphi(100); |
La respuesta correcta es la a).
| > |
5. Test resuelto del curso 2001/2002
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | ifactor(712504);ifactor(985898); igcd(712504,985898); |
| > |
| > |
| > |
| > | chrem([42,-8,25,0],[99,50,17,13]); 99*50*17*13; |
La respuesta correcta es la c).
| > |
3. Determina el número de múltiplos de 13 que hay entre el 115218 y el 369214 (ambos inclusive).
| > |
| > | c:=0: for i from 115218 to 369214 do if (i mod 13)=0 then c:=c+1 fi od: c; |
La respuesta correcta es la a).
| > |
4. Calcula el porcentaje de números primos entre el 30.000 y el 40.000 (ambos inclusive)
| > |
| > | c:=0: for i from 3*10^4 to 4*10^4 do if isprime(i) then c:=c+1 fi; od; evalf(c/10001); |
La respuesta correcta es la b).
| > |
| > |
| > | seq([n,n^(13)+1 mod 13], n=0..12); |
La respuesta correcta es la b).
| > |
6. Sean las congruencias 3x+1 congruente con 5 módulo 7 y 2x+3 congruente con 7 módulo 11.
| > |
| > | msolve(3*x+1=5,7); msolve(2*x+3=7,11); |
| > | {seq(7*i+6,i=1..100)}intersect{seq(11*i+2,i=1..100)}; |
| > |
| > |
La respuesta correcta es la c).
| > |
| > |
| > | phi(1000); |
La respuesta correcta es la a).
| > |
| > |
| > | (1513 mod 11, 1513 mod 13, 1513 mod 17); |
| > | (1206 mod 11, 1206 mod 13, 1206 mod 17); |
La respuesta correcta es la b).
9. El inverso de 7 módulo 5, el de 4 módulo 9 y el de 8 módulo 11 son:
| > |
| > | msolve(7*x=1,5);msolve(4*x=1,9);msolve(8*x=1,11); |
La respuesta correcta es la c).
10. El mcd(a,b,c) verifica que:
| > |
| > | igcd(14,67,89); igcd(14,igcd(67,89)); |
| > | igcd(1445,6785,8900); igcd(1445,igcd(6785,8900)); |
| > |
La respuesta correcta es la a).
| > |
6. Test resuelto del curso 2002/2003
1. Los números enteros 9755076 y 3489755:
a) Son relativamente primos entre sí.
b) No tienen divisores comunes.
c) Tienen 4 divisores comunes.
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | igcd(9755076,3489755); |
| > |
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | ifactor(99);ifactor(52);99*52*17*19; |
| > | chrem([42,-8,25,0],[99,52,17,19]); |
La respuesta correcta es la b).
| > |
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | listaprimos:=proc(n) local p,i,c; i:=1;c:=[]; for p from 2 to n do if isprime(p) then c:=[op(c),p]; fi; od; c; end: listaprimos(100);nops(%); |
La respuesta correcta es la a).
| > |
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | f:=n->4*n^32+4 mod 8; |
| > | seq([n,4*n^32+4 mod 8], n=0..7); |
La respuesta correcta es la b).
| > |
5. Calcula la cantidad de números primos entre los números del tipo
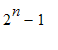 ,
,
![]() , menores que 100000.
, menores que 100000.
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | solve(2^n-1<100000,n); |
| > | floor(ln(100001)/ln(2)); |
| > | seq(2^n-1,n=2..16);2^17-1; |
| > | c:=0:for i from 2 to 16 do if isprime(2^i-1) then c:=c+1: fi; od; c; |
La respuesta correcta es la a).
| > |
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | ifactor(4536789); |
| > | phi(4536789); |
La respuesta correcta es la b) porque los múltiplos de 3 no son relativamente primos con 4536789.
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | solve(7*i+5<1000,i);floor(995/7); |
| > | c:=0: for i from 1 to floor(995/7) do if isprime(7*i+5) then c:=c+1 fi: od: c; |
La respuesta correcta es la a).
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | chrem([1,1],[5,3]); chrem([1,1],[10,3]); |
| > |
La respuesta correcta es la c).
| > |
| > |
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | f:=n->a*n+2 mod 7;simplify(f(f(n))-n); |
| > | for a from 0 to 6 do if simplify(f(f(n))-n)=0 then print(a); fi; od; |
La respuesta correcta es la c).
| > |
10. Los inversos de 3, 5 y 7 modulo 12 son respectivamente:
| > |
| > | restart; with(numtheory): |
Warning, the protected name order has been redefined and unprotected
| > | msolve(5*n-1,12); msolve(7*n-1,12); |
1
1, 1
1, 2, 1
1, 3, 3, 1
1, 4, 6, 4, 1
1, 5, 10, 10, 5, 1
1, 6, 15, 20, 15, 6, 1
Introducción a la Combinatoria con Maple
| > | with(combinat); |
Warning, the protected name Chi has been redefined and unprotected
| > |
Hay otro paquete de funciones más avanzadas, combstruct , que no emplearemos en esta práctica.
Recordamos que los conjuntos se definían con llaves.
| > | A:={1,2,3,4}; |
Y que la operación nops calculaba el número de elementos, es decir, el cardinal del conjunto A:
| > | nops(A); |
| > | C:={seq(n^2,n=-10..10)}; nops(C); |
| > | B:={1,a,b,c}; |
| > | A union B; |
| > | A intersect B; |
| > | A minus B; |
Podemos hacer un procedimiento simple para construir el conjunto producto cartesiano:
| > | cartesiano:=proc(A::set,B::set) local i,j,C: C:={}: for i from 1 to nops(A) do for j from 1 to nops(B) do C:=C union {[[op(A)][i],[op(B)][j]]} od: od: C; end: |
| > | cartesiano({1,2},{l,m}); |
| > | cartesiano({maria,juana,luisa},{pedro,pepe,juan}); |
| > |
Definimos el conjunto de los cuadrados menores que 1000.
| > | evalf(sqrt(1000)); |
| > | 32**2; |
| > | F:={seq(n^2,n=1..31)}; |
Definimos el conjunto de los múltiplos de 4 menores o iguales que 1000.
| > | G:={seq(4*n,n=1..250)}: |
Por tanto debemos calcular el cardinal de la intersección.
| > | nops(F intersect G); |
Los números enteros que cumplen ambas condiciones son exactamente:
| > | F intersect G; |
| > |
En efecto todos ellos son múltiplos de 4 y el cuadrado de un número entero.
El número de permutaciones de m elementos se calcula con numbperm :
| > | numbperm(6); |
También se puede usar el símbolo ! o la expresión factorial para calcular el factorial de un número:
| > | 6!; factorial(6); |
La función numbperm se puede aplicar a un conjunto en lugar de a su cardinal:
| > | numbperm({a,b,c,d,e,f}); |
| > | permute({a,b,c}); |
Observad que el resultado es una secuencia.
| > | randperm({a,b,c,d,e,f}); |
Si queremos introducir repeticiones , entonces debemos dar los datos con una secuencia:
| > | permute([c,o,c,o,d,r,i,l,o]): |
| > | numbperm([c,o,c,o,d,r,i,l,o]); |
Y podemos verificar que es correcto según las fórmulas de clase:
| > | 9!/(2!*3!); |
| > | multinomial(9,2,3,1,1,1,1); convert(multinomial(n,a,b,c,d),factorial); |
De esta manera las permutaciones con repetición se pueden calcular por estos dos caminos:
| > | is(numbperm([c,o,c,o,d,r,i,l,o])=multinomial(9,2,3,1,1,1,1)); |
| > |
| > | numbcomb({Maria, Juan, Eva, Luis, Teresa, Pablo},2); |
| > | binomial(6,2); |
Para ver la fórmula con la que trabaja binomial podemos usar de nuevo convert .
| > | convert(binomial(m,n),factorial); |
Si lo que queremos es obtener la lista de todas las combinaciones empleamos choose :
| > | ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set choose({Maria, Juan, Eva, Luis, Teresa, Pablo},2); |
Obsérvese que el resultado es un conjunto.
| > | numbcomb({Maria, Juan, Eva, Luis, Teresa, Pablo}); |
| > | 2^6; |
| > | ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set choose({Maria, Juan, Eva, Luis, Teresa, Pablo}); |
| > |
Podemos generar una combinación de forma aleatoria con randcomb
| > | randcomb({chocolate,vainilla,fresa,limon},2); |
| > | randcomb(5,3); |
| > |
En el último caso se eligen al azar tres números del conjunto {1,2,3,4,5} .
| > | ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set choose([a,b,a],2); |
| > | numbcomb([a,b,a],2); |
| > | binomial(2+2-1,2); |
Ya que en las combinaciones elegidas arriba, falta la pareja (b,b) .
| > | CR:=(m,n)->binomial(m+n-1,n); |
| > | CR(2,2); |
| > |
Vamos a construir una fórmula para las variaciones y para las variaciones con repetición.
| > | V:=(m,n)->binomial(m,n)*n!; |
| > | V(3,5); |
| > | V(3,3); |
| > | V2:=proc(m,n) local s,i: if n>m then s:=0 else s:=1: for i from 0 to n-1 do s:=s*(m-i): od: fi: s; end: |
| > | V2(5,3); V2(5,10); |
Y también podemos construir una fórmula para las variaciones con repetición:
| > | VR:=(m,n)->m^n; |
| > | VR(2,3); |
| > | variaciones:=proc(A,n) local C,D,i: ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set C:=[op(choose(A,n))]: D:={}: for i from 1 to nops(C) do D:= D union {op(permute([op(C[i])]))}: od: D; end: |
| > | variaciones({a,b,c,d},3); |
En efecto, se han obtenido todas:
| > | is(nops(variaciones({a,b,c,d,e},3))=V(nops({a,b,c,d,e}),3)); |
| > | variaciones({1,2,3},2); |
| > | variaciones({p,q,r,s,t,u,v},7): |
| > | is(nops(%)=7!); |
| > |
| > | partition(10); |
| > | numbpart(10); |
Y en efecto calcula el cardinal del conjunto anterior:
| > | nops(partition(10)); |
De igual manera si se quiere conseguir una partición aleatoriamente:
| > | randpart(10); |
Observa que si se repite el comando anterior:
| > | randpart(10); |
| > |
Como la elección es aleatoria, es demasiada casualidad que haya salido igual.
| > |
| > | with(combinat): |
| > | evalf(binomial(154,3)*(1/3)^3*(2/3)^(151)); |
| > |
| > |
| > | evalf(add(binomial(154,i)*(1/3)^i*(2/3)^(154-i),i=0..75)); |
La respuesta correcta es la c).
| > |
| > | seq([n,evalf(1-(2/3)^n)],n=1..10); |
La respuesta correcta es la a).
| > |
| > | evalf(add(s^2/100,s=1..100)); |
La respuesta correcta es la a).
| > |
| > |
| > | c:=0; for i from 1 to 5000 do if isprime(i) then c:=c+1 fi; od; evalf(c/5000); |
La respuesta correcta es la c).
| > |
| > | evalf(1/(numbperm([c,o,c,o,d,r,i,l,o])*numbperm([a,b,r,a,c,a,d,a,b,r,a]))); |
La respuesta correcta es la b).
| > |
| > | binomial(11,6)*6!*5!; |
La respuesta correcta es la c).
| > |
| > | f:=n->1-(binomial(365,n)*n!/365^n); |
| > | seq([n,evalf(f(n))],n=30..40); |
| > |
| > |
| > | A:={seq(i^2,i=1..100)}: B:={seq(i^3,i=1..100)}: nops(A intersect B); |
La respuesta correcta es la a).
| > |
| > | restart; C:={seq(5*n,n=1..2000)}: E:={seq(7*n,n=1..2000)}: nops(C minus E); |
| > | evalf(10000/7); |
| > | A:={seq(7*i,i=1..1428)}: |
| > | B:={seq(2*i,i=1..5000)}: |
| > | C:={seq(3*i,i=1..3333)}: |
| > | nops(A minus B minus C); |
| > |
La respuesta correcta es la b)
| > | restart: with(combinat): |
Warning, the protected name Chi has been redefined and unprotected
2.- Determinar cuántos subconjuntos de menos de 5 elementos (de 0 a 4 elementos) tiene el conjunto
| > | E:={a,b,c,d,f,e,r,t,y,n,l}: |
| > |
| > | nops(E); |
| > | c:=binomial(11,0): for i from 1 to 4 do c:=c+binomial(11,i): od: c; |
| > |
La respuesta correcta es la c).
| > | 54*53*52*binomial(51,3); |
| > |
La respuesta correcta es la b).
| > | c:=0: for i from 1 to 10000 do if isprime(i) then c:=c+1: fi: od: c; |
| > | evalf((1229/10^4)^2); |
| > |
La respuesta correcta es la b).
| > | restart: with(combinat): |
Warning, the protected name Chi has been redefined and unprotected
| > | p:=n->binomial(n,3)/binomial(357,3); |
| > | i:=0: while(evalf(p(i))<1/3) do i:=i+1: od: i; |
| > | evalf(p(247)); evalf(p(248)); evalf(p(249)); |
| > |
La respuesta correcta es la a).
| > | numbperm([s,e,m,a,f,o,r,o,s]); |
| > |
La respuesta correcta es la c).
| > | A:={1,2,3,4,5,e,r,t,y,u,i,o,p}: B:={1,2,3,4,5,e,r,t,g,y,u,h,j,l}: |
| > | ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set nops(choose(A,3) intersect choose(B,3)); |
| > | ### WARNING: combinat[choose] with numeric first parameter now returns a sorted list rather than a set nops(choose(A intersect B,3)); |
| > |
La respuesta correcta es la a).
8.- Cuántos números se pueden representar en el sistema binario con 10 dígitos.
b) Más de 1500 y menos de 2000
c) Más de 1000 y menos de 1100
| > | 2**10; |
| > |
La respuesta correcta es la c).
| > | 27*27*37*37*37*10*10; |
| > |
La respuesta correcta es la c).
10.- Dados dos números naturales m y n decimos que m es ascendente de n si se verifica que
| > | m**3=n**2; |
| > | c:=0: for m from 1 to 1000 do for n from 1 to 1000 do if m^3=n^2 then c:=c+1: fi: od: od: evalf(c/1000); |
| > |
| > |
| > |
La respuesta correcta es la a).
elegir y ordenar los primeros 4 coches que se van a arreglar.
| > | restart;with(combinat):V:=(m,n)-> binomial(m,n)*n!; |
Warning, the protected name Chi has been redefined and unprotected
| > | V(10,4); |
La respuesta correcta es la c).
| > |
| > | restart;with(combinat): numbperm([A,L,E,S,S,A,N,D,R,A]); |
Warning, the protected name Chi has been redefined and unprotected
La respuesta correcta es la c).
| > |
3) Determinar cuantos posibles resultados pueden acontecer al lanzar 25 monedas simultáneamente.
| > | restart;with(combinat): binomial(26,25); |
Warning, the protected name Chi has been redefined and unprotected
La respuesta correcta es la c).
| > |
dos últimos han de ser números.
| > | 54*54*54*64*64*64*10*10; |
La respuesta correcta es la b).
| > |
a) la probabilidad de S intersección con S' es 0.4
b) S y S' no son sucesos independientes.
c) S y S' son sucesos independientes.
| > | 0.5*0.8; |
Pero p(S|S') no es igual a p(S).
La respuesta correcta es la b).
| > |
| > | restart;with(combinat): |
Warning, the protected name Chi has been redefined and unprotected
| > | floor(10^(4/3)); |
| > | A:={seq(i^3,i=1..21)}:nops(A); |
| > | solve(3+5*k<=10^4,k); |
| > | floor(9997/5); |
| > | B:={seq(3+5*k,k=0..1999)}:nops(B); |
| > | nops(A intersect B)/10^4; |
| > |
| > | restart: with(combinat): |
Warning, the protected name Chi has been redefined and unprotected
| > | p:=n->binomial(n,5)/binomial(32,5); |
| > | i:=0: while(evalf(p(i))<1/5) do i:=i+1: od: i; |
| > | evalf(1/5);evalf(p(23)); evalf(p(24)); |
La respuesta correcta es la a).
| > |
que la suma de los resultados de ambos dados sea 7.
| > |
| > | restart;with(combinat): suma:=partition(7); |
Warning, the protected name Chi has been redefined and unprotected
| > | c:=0: suma2:=[]: for i from 1 to nops(suma) do if nops(suma[i])=2 then suma2:=[op(suma2),suma[i]]: c:=c+1; fi: od; c;suma2; |
| > |
| > | p:=6/36; |
La respuesta correcta es la a).
| > |
9) Sea un experimento de Bernoulli con probabilidad de éxito p=1/4.
Calcula la probabilidad de obtener exactamente 53 éxitos al repetir el experimento 200 veces.
| > |
| > | restart;with(combinat): |
Warning, the protected name Chi has been redefined and unprotected
| > | evalf(binomial(200,53)*((1/4)^53)*((3/4)^(147))); |
La respuesta correcta es la b).
| > |
| > |
| > | restart;with(combinat):with(numtheory): |
Warning, the protected name Chi has been redefined and unprotected
Warning, the protected name order has been redefined and unprotected
| > | phi(567)/567; |
La respuesta correcta es la b).
| > | #fin |
(Libro de referencia: "EXPLORING DISCRETE MATHEMATICS WITH MAPLE" de K.H.Rosen, McGraw Hill 1997 )
Maple tiene una librería de comandos relacionados con la teoría de grafos denominada networks:
| > | restart; with(networks); |
| > | G1:=new(): |
A continuación añadimos los vértices al grafo, por ejemplo:
| > | addvertex({Mostoles,Alcorcon,Fuenlabrada,Vicalvaro,Pozuelo},G1); |
| > | addedge({{Mostoles,Alcorcon},{Mostoles,Fuenlabrada},{Alcorcon,Fuenlabrada},{Fuenlabrada,Vicalvaro},{Alcorcon,Pozuelo},{Vicalvaro,Pozuelo},{Alcorcon,Vicalvaro}},G1); |
Para saber cuáles son las aristas de nuestro grafo utilizamos el comando ends o edges :
| > | ends(G1); edges(G1); |
Y para representar gráficamente el grafo utilizamos el comando draw :
| > | draw(G1); |
| > | edges({Mostoles,Alcorcon},G1); edges({Pozuelo, Alcorcon},G1); edges({Mostoles,Pozuelo},G1); |
| > | draw(Linear([Mostoles,Alcorcon],[Fuenlabrada,Vicalvaro,Pozuelo]),G1); |
El comando vertices se emplea para recuperar los vértices del grafo:
| > | vertices(G1); |
El comando vdegre nos permite obtener el grado de cualquier vértice:
| > | vdegree(Mostoles,G1); |
Si quisiéramos trabajar con digrafos, las aristas deben ser un conjunto de pares ordenados:
| > | D1:=new(): addvertex({Mostoles,Alcorcon,Fuenlabrada,Vicalvaro,Pozuelo},D1): addedge({[Mostoles,Alcorcon],[Mostoles,Fuenlabrada],[Alcorcon,Fuenlabrada],[Fuenlabrada,Vicalvaro],[Alcorcon,Pozuelo],[Vicalvaro,Pozuelo],[Alcorcon,Vicalvaro],[Vicalvaro,Alcorcon]},D1): vertices(D1); edges(D1); ends(D1); |
| > | draw(D1); |
| > | M1:=new(): addvertex({Mostoles,Alcorcon,Fuenlabrada,Vicalvaro,Pozuelo},M1): addedge([{Mostoles,Mostoles},{Mostoles,Alcorcon},{Mostoles,Alcorcon},{Mostoles,Fuenlabrada},{Alcorcon,Fuenlabrada},{Fuenlabrada,Vicalvaro},{Alcorcon,Pozuelo},{Vicalvaro,Pozuelo},{Alcorcon,Vicalvaro}],M1): vertices(M1); edges(M1); ends(M1); |
De nuevo el dibujo no es ilustrativo:
| > | draw(M1); |
Petersen (no visto en clase, mira cómo es más abajo), los bipartidos completos, etc.
| > | draw(complete(5)); |
| > | draw(cycle(7)); |
| > | draw(cube(3)); |
| > | draw(petersen()); |
| > | draw(complete(2,6)); |
| > | draw(complete(2,5)); |
| > | draw(Linear([1,2],[3,4,5,6,7]),complete(2,5)); |
| > | adjacency(complete(4)); |
| > | incidence(complete(4)); |
| > | adjacency(G1); |
| > | G2:=new(): |
| > | addvertex({v1,v2,v3,v4,v5,v6,v7,v8,v9},G2): |
| > | addedge({{v1,v2},{v1,v3},{v5,v6},{v6,v7},{v7,v8},{v8,v9}},G2): |
| > | components(G2); |
| > | draw(G2); |
Grafos eulerianos y hamiltonianos
Dado un grafo la función degreeseq da la lista de los grados de sus vértices:
| > | degreeseq(G2); |
Entonces podemos crear un procedimiento para saber si un grafo conexo es euleriano:
| > | Euleriano:=proc(G::graph) local c,i,r: c:=degreeseq(G):i:=1: while i<nops(c)+1 do if (c[i] mod 2)<>0 then i:=nops(c)+2: else i:=i+1: fi: od: if i=nops(c)+2 then r:="no euleriano": else r:="euleriano": fi: r; end: |
| > | Euleriano(cycle(5)); |
| > | Euleriano(complete(4)); |
| > | Euleriano(complete(5)); |
| > |
Observa que las aristas deben entrar como una lista:
| > | new(G3): addvertex({a,b,c,d,y,z},G3); addedge( [{a,b},{a,d},{b,c},{b,y},{c,z},{d,y},{y,z}], weights=[4,2,3,3,2,3,1], G3); |
Al pintarlo no señala las etiquetas.
| > | draw(G3); |
Pero el comando eweight (edge weight) recupera el peso de cada una de sus aristas.
| > | eweight(e1,G3); |
| > |
| > | A1:=shortpathtree(G3,a): draw(A1); |
| > |
| > | vweight(z,A1); |
| > | vweight(y,A1); |
| > | vweight(d,A1); |
| > | with(linalg): |
Warning, the names charpoly and rank have been redefined
Warning, the protected names norm and trace have been redefined and unprotected
| > | A:= matrix([[1,-alpha,2/3],[-1,0,1],[beta/3,2,-1]]); |
Que también se puede escribir señalando primero el tamaño de la matriz:
| > | matrix(3,3,[1,-alpha,2/3,-1,0,1,beta/3,2,-1]); |
| > | transpose(A); |
Podemos sumar y restar matrices. Para que la matriz resultado se escriba en pantalla se usa evalm .
| > | B:= matrix([[1,2,1],[1,1,0],[-1,0,1]]); |
| > | A+B; |
| > | evalm(A+B); |
| > | C:= multiply(A,B); |
| > | evalm(A&*B); |
| > | evalm(A &* B - 1/3*C); |
Podemos hacer potencias de matrices:
| > | evalm(A^3); |
| > | F:=evalm(B^7); |
| > | F[3,3]; |
| > | rowdim(F);coldim(F); |
| > |
Ejercicios previos al test de evaluación
| > | restart; with(networks): |
1.1. ¿Cómo se puede calcular el número de aristas de un grafo? ¿Y el número de vértices?.
| > | G:=complete(9): |
| > | nops(vertices(G)); |
| > | nops(edges(G)); |
1.2. Escribir un procedimiento que calcule la sucesión de los grados de un grafo.
| > | H:=new(): |
| > | addvertex({a1,a2,a3,a4,a5,a6,a7},H): |
| > | addedge({{a1,a2},{a1,a3},{a6,a7},{a5,a6}},H): |
| > | draw(H); |
| > | degreeseq(H); |
| > | L:=[op(vertices(H))]; vdegree(L[1],H); |
| > | for i from 1 to nops(L) do c[i]:=vdegree(L[i],H):od: seq(c[j],j=1..nops(L)); |
| > |
1.3. Escribir un procedimiento que calcule la suma de los grados de todos los vértices de un grafo.
Simplemente sumar los elementos de la lista que da degreeseq.
1.4. Emplearlo para verificar que dicha suma es siempre el doble del número de aristas del grafo.
1.5. Escribir un procedimiento que calcule el número de vértices con grado impar de un grafo.
| > | restart; with(linalg):with(networks): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the names charpoly and rank have been redefined
| > | Vertices:=proc(A::matrix) local L,i: L:={}: for i from 1 to rowdim(A) do L:=L union {i}: od: L; end: |
| > | Vertices(matrix(2,2,[0,1,1,0])); |
| > | Aristas:=proc(A::matrix) local L,i,j: L:={}: for i from 1 to rowdim(A) do for j from 1 to coldim(A) do if A[i,j]=1 then L:=L union {{i,j}}: fi: od: od: L; end: |
| > | Aristas(matrix(2,2,[0,1,1,0])); |
| > | grafo:=proc(A::matrix) local G: G:=new(): addvertex(Vertices(A),G): addedge(Aristas(A),G): G; end: |
| > | draw(grafo(matrix(2,2,[0,1,1,0]))); |
| > | M:=matrix(5,5,[0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0]); |
| > | draw(grafo(M)); |
| > | M:=matrix(4,4,[0,1,0,0,1,0,1,1,0,1,0,0,0,1,0,0]); |
El grafo que la tiene como matriz de adyacencias es:
| > | draw(grafo(M)); |
| > |
| > |
| > | with(networks): |
| > | M:=adjacency(cube(6)): |
| > | with(linalg): coldim(M); |
Warning, the names charpoly and rank have been redefined
| > | c:=0; for i from 1 to 64 do for j from 1 to 64 do c:=c+M[i,j] od; od; c; |
| > |
| > |
| > | N:=incidence(cube(6)): |
| > | coldim(N); rowdim(N); |
| > | c:=0; for i from 1 to 64 do for j from 1 to 192 do c:=c+N[i,j] od; od; c; |
| > |
| > |
| > | M:=adjacency(complete(3,3)): |
| > | with(linalg): coldim(M); |
| > | c:=0; for i from 1 to 6 do for j from 1 to 6 do c:=c+M[i,j] od; od; c; |
| > | 384+18; |
| > |
| > |
| > | restart; with(linalg): A:=matrix([[0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1], [1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0], [1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0], [1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0], [1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1], [1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1], [1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0], [1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0], [1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0], [1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0]]); |
Warning, the protected names norm and trace have been redefined and unprotected
| > |
| > |
| > |
| > | evalm(A^3)[1,3]; |
| > |
| > |
| > | 25-13; |
| > |
| > |
| > | with(networks): G:=new(): |
Warning, the names charpoly and rank have been redefined
| > | addvertex({1,2,3,4,5,6,7,8,9},G); |
| > | addedge({{1,2},{1,3},{2,4},{2,5},{3,6},{3,7},{7,8},{7,9}},G); |
| > | draw(G); |
| > |
| > |
10.- ¿Cuántos vértices de grado impar tiene la unión disjunta
![]() y
y
![]() ?
?
| > |
Los vértices de cada uno de los grafos del enunciado son de grado 4, por tanto respuesta c).
| > | restart: with(networks): with(linalg): |
Warning, the names charpoly and rank have been redefined
Warning, the protected names norm and trace have been redefined and unprotected
| > | M:=matrix([[0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1], [0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1], [1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1], [1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0], [1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1], [1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0], [0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1], [0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1], [0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0], [0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1], [1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1], [0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0], [1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1], [1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0], [1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0], [1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0], [0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0], [1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1], [0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1], [0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1], [0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0], [0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0], [0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0], [0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0], [0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1], [1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1], [0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0], [1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1], [1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0], [1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0], [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0], [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1], [0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0], [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1], [0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1], [0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0]]): |
1.-Sea un grafo simple G una de cuyas matrices de ayacencias es M:
a) G tiene 50 vértices y 601 aristas.
b) G tiene 40 vértices y 550 aristas.
c) G tiene 50 vértices y 400 aristas.
El número de vértices de G es el número de filas (o de columnas) de M:
| > | rowdim(M); |
| > | S:=0: for i from 1 to 50 do: for j from 1 to 50 do: S:=S+M[i,j]: od: od: S/2; |
| > |
Por tanto tiene 601 aristas. La respuesta correcta es la a).
2.- Determinar el grado del vértice tercero en la ordenación de los vértices que define la matriz M.
El grado del vértice tercero es la suma de los elementos de la fila (o columna) tercera
| > | gr(3):=0: for t from 1 to 50 do: gr(3):=gr(3)+M[3,t]: od: gr(3); |
| > |
La respuesta correcta es la c).
3.- Determinar el número de caminos de longitud 3 que hay entre el vértice 40 y el 50 del grafo G.
La matriz M^3 es la que contiene dicha información:
| > | evalm(M^3)[40,50]; |
| > | evalm(M^3)[50,40]; |
La respuesta correcta es la b)
b) tiene dos componentes conexas
c) no se puede saber si es conexo o no
| > | C:=evalm(M^2): |
| > | S:=0: for z from 1 to 50 do for t from 1 to 50 do if C[z,t]=0 then S:=S+1: fi: od: od: S; |
| > |
La respuesta correcta es la a).
b) no es un árbol porque es no conexo
c) no es un árbol porque contiene ciclos
Como un árbol de n vértices tiene n-1 aristas y G es conexo (con 50 vértices y 600 aristas)
entonces la respuesta correcta es la c).
6.- El grafo completo K6 verifica .
a) es conexo tiene 6 vértices y 15 aristas, el grado de cada vértice es 6.
b) es conexo tiene 6 vértices y 15 aristas, el grado de cada vértice es 5.
c) es conexo tiene 6 vértices y 21 aristas, el grado de cada vértice es 5.
| > | restart;with(networks): |
| > | nops(vertices(complete(6))); |
| > | nops(ends(complete(6))); |
| > | degreeseq(complete(6)); |
| > | components(complete(6)); |
La respuesta correcta es la b).
| > | H:=new(): |
| > | addvertex({seq(i,i=1..30)},H): |
| > | addedge({{1,2},{1,4},{3,2},{5,6},{21,12},{21,22},{4,20},{1,7},{8,9},{1,5},{1,20},{3,24},{21,3},{11,24},{15,26},{16,20},{10,20},{1,29},{21,6},{11,4},{13,22},{15,16},{17,19},{19,20},{14,7},{13,7}},H): |
7.- Sea el grafo simple H definido arriba. Dicho grafo verifica:
b) no es conexo porque tiene tres componentes conexas
c) no es conexo porque tiene ocho componentes conexas
| > | draw(H); |
Vemos con el dibujo que es no conexo. Podemos computar el número de sus componentes conexas.
| > | nops(components(H)); |
| > |
La respuesta correcta es la c).
8.- El grado del vértice de mayor grado de H y el del de menor grado son respectivamente:
| > | degreeseq(H); |
| > |
La respuesta correcta es la a).
9.- Sea el subgrafo L de H que forma la componente conexa con mayor número de vértices.
b) L no es euleriano porque es no conexo
| > | components(H); |
| > | L:=new(): |
| > | addvertex({3, 26, 22, 24, 20, 21, 16, 17, 19, 13, 14, 15, 10, 11, 12, 6, 7, 1, 2, 4, 5, 29},L): |
| > | addedge({{1,2},{1,4},{3,2},{5,6},{21,12},{21,22},{4,20},{1,7},{1,5},{1,20},{3,24},{21,3},{11,24},{15,26},{16,20},{10,20},{1,29},{21,6},{11,4},{13,22},{15,16},{17,19},{19,20},{14,7},{13,7}},L): |
| > | degreeseq(L); |
| > |
| > |
Como hay vértices de grado impar la respuesta correcta es la c).
10.- Determina el número de vértices de grado impar de L.
a) L tiene 10 vértices de grado impar
b) L tiene 11 vértices de grado impar
c) L tiene 12 vértices de grado impar
La respuesta correcta es la a).
| > | S:=0: for k from 1 to nops(vertices(L)) do if degreeseq(L)[k] mod 2<>0 then S:=S+1: fi: od: S; |
| > |
| > |
| > | restart: with(networks): with(linalg): |
Warning, the names charpoly and rank have been redefined
Warning, the protected names norm and trace have been redefined and unprotected
| > | A:=matrix([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]): |
| > |
1. Sea el grafo simple G=(V,E) una de cuyas matrices de adyacencias es A.
a) G tiene 45 vértices y 506 aristas.
b) G tiene 60 vértices y 206 aristas.
c) G tiene 45 vértices y 1012 aristas.
| > | rowdim(A); |
| > | s:=0: for i from 1 to rowdim(A) do for j from i to coldim(A) do s:=s+A[i,j]: od: od: s; |
| > |
La respuesta correcta es la a).
a) tiene 23 vértices de grado impar.
b) tiene 22 vértices de grado impar.
c) tiene 24 vértices de grado par.
| > | for i from 1 to rowdim(A) do g[i]:=add(A[i,j],j=1..rowdim(A)): od: seq(g[i],i=1..rowdim(A)); |
| > | s:=0: for i from 1 to rowdim(A) do if g[i] mod 2 =1 then s:=s+1 fi od: s; |
| > |
La respuesta correcta es la b).
3. El número de caminos de longitud 27 uniendo el vértice 1 y el 22 del grafo G es
| > | evalm(A^27)[1,22]; |
| > |
La respuesta correcta es la c).
4. Señalar la respuesta correcta:
b) el grafo G tiene dos componentes conexas.
c) el grafo G tiene más de tres componentes conexas .
| > | Vertices:=proc(A::matrix) local L,i: L:={}: for i from 1 to rowdim(A) do L:=L union {i}: od: L; end: |
| > | Aristas:=proc(A::matrix) local L,i,j: L:={}: for i from 1 to rowdim(A) do for j from 1 to rowdim(A) do if A[i,j]=1 then L:=L union {{i,j}}: fi: od: od: L; end: |
| > | grafo:=proc(A::matrix) local G: G:=new(): addvertex(Vertices(A),G): addedge(Aristas(A),G): G; end: |
| > | G:=grafo(A): |
| > | nops(components(G)); |
| > |
La respuesta correcta es la a).
El número total de caminos de longitud 3 es:
| > | evalm(A^3)[1,45]; |
Obsérvese que 1 y 45 son adyacentes:
| > | A[1,45]; |
El número de caminos no simples de la forma 1a1(45) es el grado del vértice 1:
| > | L:=seq(A[1,i],i=1..rowdim(A)): g:=0: for i from 1 to rowdim(A) do g:=g+L[i]: od: g; |
El número de caminos no simples de la forma 1(45)b(45) es el grado del vértice 45:
| > | L:=seq(A[45,i],i=1..rowdim(A)): g:=0: for i from 1 to rowdim(A) do g:=g+L[i]: od: g; |
De esta forma, estamos contando el camino 1(45)1(45) dos veces: cuando a = 45 y cuando b=1.
El número de caminos simples es
| > | 506-23-22+1; |
La respuesta correcta es la a)
| > |
La sucesión de los grados de los vértices de G es:
| > | degreeseq(G); |
Si G es bipartido completo, tiene que ser isomorfo a
![]() y tener
y tener
| > | 22*23; |
Para verificar si G es bipartido, ordenamos sus vértices
| > | L:=[op(vertices(G))]; |
y definimos las sucesiones
![]() y
y
![]() de los vértices de grado 22 y 23, respectivamente.
de los vértices de grado 22 y 23, respectivamente.
| > | j:=1: for i from 1 to 45 do if vdegree(L[i],G)=22 then a[j]:=L[i]; j:=j+1; fi; od; |
| > | s1:=seq(a[i],i=1..23); |
| > | j:=1: for i from 1 to 45 do if vdegree(L[i],G)=23 then b[j]:=L[i]; j:=j+1; fi; od; |
| > | s2:=seq(b[i],i=1..22); |
Finalmente, podemos dibujar G:
| > | draw(Linear([s1],[s2]),G); |
| > |
La respuesta correcta es la b).
| > |
c) no se puede saber si es o no Euleriano.
| > |
| > |
Sea el grafo simple H=(W,F) donde:
| > | W:={3,5,9,45}; |
| > | F:={[3,5],[5,45],[9,45]}; |
a) el grafo resultado de unir G y H tiene 1 arista más que G.
b) el grafo resultado de unir G y H tiene 3 aristas más que G.
c) el grafo resultado de unir G y H tiene las mismas aristas que G.
| > | A[3,5]; A[5,45]; A[9,45]; |
La respuesta correcta es la a).
| > |
9. Sea el grafo completo K2. El producto cartesiano GxK2 tiene
b) 45 vértices y 1012 aristas.
Si G=(V,E), el cardinal del conjunto de aristas del producto cartesiano es 2|E|+|G| :
| > | 2*506+45; |
La respuesta correcta es la c).
| > |
La respuesta correcta es la b).
| > | #fin |
| > | restart; A:={a,b,c,d}; R:={[a,a],[b,b],[c,c],[d,d],[a,b],[b,c],[a,c]}; |
| > | N:=subs(a=1,b=2,c=3,d=4,R); |
Ahora mediante plot podemos representar la secuencia de los pares de N
| > | plot([op(N)],x=0..4,y=0..4,style=point); |
| > | with(networks): |
| > | G:=new(): |
| > | addvertex(A,G); |
| > | addedge(R,G); |
| > | draw(G); |
Tampoco la matriz de adyacencias de G recoge toda esta información.
| > | adjacency(G); |
| > | with(linalg): |
Warning, the names charpoly and rank have been redefined
Warning, the protected names norm and trace have been redefined and unprotected
| > | MatrizRelacion:=proc(D::list,R::set([anything,anything])) local i,j,L; L:=[]; for i from 1 to nops(D) do for j from 1 to nops(D) do if member([[op(D)][i],[op(D)][j]],R) then L:=[op(L),1] else L:=[op(L),0]; fi; od; od; evalm(matrix(nops(D),nops(D),L)); end: |
| > | M:=MatrizRelacion([a,b,c,d],R); |
Observamos que si se toma el conjunto :
| > | B:={2,a,3}: |
Y hacemos una lista con los elementos del conjunto:
| > | [op(B)]; |
| > | RelacionMatriz:=proc(M::matrix(square)) local i,j,R; R:={}; for i from 1 to coldim(M) do for j from 1 to coldim(M) do if(M[i,j]=1) then R:=R union {[i,j]}; fi; od; od; RETURN(R); end: |
| > | S:=RelacionMatriz(M); |
| > | subs(1=a,2=b,3=c,4=d,S); |
| > |
| > |
Estudio de las propiedades de una relación
| > | p1:=plot(x,x=0..4): |
| > | p2:=plot([op(N)],style=point): |
| > | plots[display](p1,p2); |
| > | Diagonal:={seq([[op(A)][i],[op(A)][i]],i=1..nops(A))}; |
| > | Diagonal minus R; |
| > | M := matrix([[1, 1, 1, 0], [0, 1, 1, 0], [0, 0, 1, 0], [0, 0, 0, 1]]); |
| > | seq(M[i,i],i=1..nops(A)); |
No es difícil diseñar un procedimiento que lo compruebe sobre una matriz:
| > | Mref:=proc(M::matrix) local j,S,r: S:=0: for j from 1 to coldim(M) do S:=S+M[j,j]: od: if S=coldim(M) then r:="reflexiva": else r:="no reflexiva": fi: r; end: |
| > | Mref(M); |
| > | Mref(matrix(2,2,[1,0,0,0])); |
| > |
Propiedad simétrica y antisimétrica
| > | A:={1,2,3,4,5}; R:={[1,2],[2,1],[1,3],[3,1],[4,4],[5,5]}; |
La representamos mediante una tabla.
| > | p1:=plot([op(R)],x=0..5,y=0..5,style=point): |
| > | p2:=plot(x,x=0..5): |
| > | plots[display]({p1,p2}); |
| > | S:={seq([op(R)[i][2],op(R)[i][1]],i=1..nops(R))}; |
| > | R minus S; S minus R; |
Por tanto se tiene la simetría de la relación.
Para comprobar si es antisimétrica el conjunto R intersección S debe estar contenido en la diagonal.
| > | Diagonal:={seq([[op(A)][i],[op(A)][i]],i=1..nops(A))}: |
| > | (R intersect S) minus Diagonal; |
Sobre el digrafo se trataría de comprobar:
Sobre la matriz, para la propiedad simétrica, se trata de comprobar si es una matriz simétrica:
| > | M:=MatrizRelacion([1,2,3,4,5],R); |
| > | with(linalg): evalm(M-transpose(M)); |
Esto se puede escribir en un procedimiento:
| > | Msim:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M-transpose(M)): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 then S:=1: fi: od: od: if S=1 then r:="no simetrica" else r:="simetrica" fi: r; end: |
| > | Msim(M); |
| > | Msim(matrix(2,2,[1,0,1,0])); |
| > | Mantisim:=proc(M::matrix) local N,S,i,j,r: S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if M[i,j]=1 and M[j,i]=1 and i<>j then S:=1: fi: od: od: if S=1 then r:="no antisimetrica" else r:="antisimetrica" fi: r; end: |
| > | Mantisim(M); |
Si tomamos la matriz de una relación antisimétrica por ejemplo:
| > | A:=matrix(4,4,[1,1,1,1,0,1,1,1,0,0,1,1,0,0,0,1]); |
| > | Mantisim(A); |
| > |
La representación gráfica no aporta ningún método reseñable para comprobar la transitividad.
| > | Transitiva:=proc(A::list,R::set) local u,v,w; for u from 1 to nops(A) do for v from 1 to nops(A) do for w from 1 to nops(A) do if(member([A[u],A[v]],R) and member([A[v],A[w]],R) and not member([A[u],A[w]],R)) then RETURN(false); fi; od; od; od; RETURN(true); end: |
| > | A:=[a,b,c,d]; R:={[a,a],[a,b],[b,a],[b,c],[a,c]}; |
| > | Transitiva(A,R); |
| > | Matrizdeunosyceros:=proc(M::matrix) local i,j,Mat; Mat:=matrix(rowdim(M),coldim(M),0); for i from 1 to rowdim(M) do for j from 1 to coldim(M) do if(M[i,j]<>0) then Mat[i,j]:=1; fi; od; od; RETURN(eval(Mat)); end: |
| > | M:=matrix(3,3,[1,1,1,2,1,3,0,9,4]); |
| > | Matrizdeunosyceros(M); |
Por tanto dada la matriz de una relación:
| > | M:=matrix(3,3,[1,1,1,0,1,0,0,1,1]); |
Calculamos la matriz de unos y ceros del cuadrado de M
| > | Matrizdeunosyceros(evalm(M^2)); |
Como son iguales la relación es transitiva.
Podemos escribir un procedimiento:
| > | Mtrans:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M^2): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 and M[i,j]=0 then S:=1: fi: od: od: if S=1 then r:="no transitiva" else r:="transitiva": fi:r; end: |
| > | Mtrans(M); |
| > | A:=matrix(4,4,[1,1,1,1,0,0,0,0,1,0,1,0,1,0,0,0]); |
| > | Mtrans(A); |
| > | evalm(A^2); |
Con, en efecto, entradas no nulas con respecto a A.
| > |
{(a,a): a elemento de A}. Por tanto se trata simplemente de la unión de R y dicha diagonal.
| > | A:={a,s,d,f}; R:={[a,s],[a,d],[d,d],[d,f],[s,f]}; |
| > | Diagonal:={seq([op(A)[i],op(A)[i]],i=1..nops(A))}; |
| > | R union Diagonal; |
| > | Q:=MatrizRelacion([a,s,d,f],R); |
| > | I4:=diag(1,1,1,1); |
| > | Matrizdeunosyceros(evalm(Q+I4)); |
| > | A:={a,s,d,f}; R:={[a,s],[a,d],[d,d],[d,f],[s,f]}; |
| > | S:={seq([op(R)[i][2],op(R)[i][1]],i=1..nops(R))}; |
La clausura simétrica es simplemente hacer la unión:
| > | R union S; |
| > | Q:=MatrizRelacion([a,s,d,f],R); |
| > | evalm(Q+transpose(Q)); |
| > | C:=Matrizdeunosyceros(%); |
| > | evalm(C-transpose(C)); |
| > | A:={a,s,d,f,g}; R:={[a,s],[a,d],[d,d],[d,f],[s,f],[f,g],[g,g]}; |
| > | Q:=MatrizRelacion([a,s,d,f,g],R); |
| > | Matrizdeunosyceros(evalm(add(Q^n,n=1..5))); |
El otro algoritmo que se presentaba es el Algoritmo de Warshall que reduce la complejidad:
| > | Warshall:=proc(M::matrix) local i,j,k,W,n; W:=matrix(rowdim(M),coldim(M),[seq(seq(M[i,j],j=1...coldim(M)),i=1..coldim(M))]): n:=coldim(M); for k from 1 to n do for i from 1 to n do for j from 1 to n do W[i,j]:=W[i,j]+(W[i,k]*W[k,j]); od; od; od; Matrizdeunosyceros(W); end: |
| > | Warshall(Q); |
| > | restart; A:={a,b,c,d,e,f,g,h,i,j}; |
| > | R:={[a,b],[a,c],[b,b],[c,b],[c,c],[a,f],[g,h],[h,i],[h,j],[j,i],[j,a],[a,a],[d,d],[j,f],[e,e],[f,j],[g,g],[j,j],[i,i],[e,b],[e,a],[f,f],[h,h]}; |
| > |
| > | with(linalg): MatrizRelacion:=proc(D::list,R::set([anything,anything])) local i,j,L; L:=[]; for i from 1 to nops(D) do for j from 1 to nops(D) do if member([[op(D)][i],[op(D)][j]],R) then L:=[op(L),1] else L:=[op(L),0]; fi; od; od; evalm(matrix(nops(D),nops(D),L)); end: |
Warning, the protected names norm and trace have been redefined and unprotected
| > |
| > | Q:=MatrizRelacion([a,b,c,d,e,f,g,h,i,j],R); |
| > |
| > |
| > |
| > | Matrizdeunosyceros:=proc(M::matrix) local i,j,Mat; Mat:=matrix(rowdim(M),coldim(M),0); for i from 1 to rowdim(M) do for j from 1 to coldim(M) do if(M[i,j]<>0) then Mat[i,j]:=1; fi; od; od; RETURN(eval(Mat)); end: |
| > | M:=Matrizdeunosyceros(evalm(add(Q^n,n=1..10))); |
| > | c:=0; for i from 1 to 10 do for j from 1 to 10 do c:=c+M[i,j] od; od; c; |
| > |
| > |
| > | seq(Matrizdeunosyceros(evalm(Q+transpose(Q)))[7,i],i=1..10); |
Luego la respuesta correcta es la b).
| > |
4.- Sea la matriz M definida abajo:
| > |
| > | M:=matrix(11,11,[0,1,1,1,1,1,1,1,1,1,1,1,0,1,0,1,0,1,0,1,0,1,1,1,0,0,0,1,0,0,1,0,0,1,0,0,0,1,1,2,1,1,0,0,1,1,0,1,0,1,0,0,0,0,0,1,0,1,1,1,0,1,0,0,0,1,1,1,0,2,0,1,0,1,1,1,1,1,0,0,1,0,0,1,0,1,0,0,1,1,1,1,0,0,1,1,0,0,0,1,0,0,0,0,0,1,0,0,0,0,1,1,0,0,0,1,1,0,0,0,0]); |
| > |
| > |
5.- La relación (B,S) definida abajo:
| > |
| > | B:={1,2,3,4,5,6,7,8,9}; S:={[1,1],[1,2],[1,3],[1,4],[5,6],[5,7],[5,8],[1,5],[1,6],[1,7],[1,8],[1,9],[2,2],[2,3],[2,4],[2,8],[2,9],[3,3],[3,4],[3,5],[3,6],[3,7],[3,8],[3,9],[4,4],[4,5],[4,6],[4,7],[4,8],[4,9],[5,5],[5,9],[6,6],[6,7],[6,8],[6,9],[7,7],[7,8],[7,9],[2,5],[2,6],[2,7],[8,8],[8,9],[9,9]}; |
| > |
| > |
| > |
6.- La clausura simétrica de la relación anterior es:
| > |
| > |
| > |
| > |
7.- Sea la matriz N definida más abajo,
| > |
| > | N:=Matrizdeunosyceros(M); |
| > | evalm(Matrizdeunosyceros(evalm(N^2))-N); |
| > |
| > |
| > |
| > |
| > |
| > | X:=matrix(4,4,[1,1,a,0,1,1,b,0,0,0,a,1,0,0,1,0]); |
| > | evalm(X^2); |
| > |
| > |
| > | evalm(X-transpose(X)); |
La respuesta correcta es la a).
| > |
| > | restart: with(linalg): |
Warning, the protected names norm and trace have been redefined and unprotected
| > | M:=matrix([[0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1], [0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1], [0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1], [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0], [1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1], [1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0], [0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1], [0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1], [0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0], [0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1], [1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1], [0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0], [1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1], [1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0], [1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0], [1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0], [0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0], [1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1], [0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1], [0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1], [0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0], [0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0], [0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0], [1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0], [0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0], [0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1], [1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1], [0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0], [1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1], [1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0], [1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0], [0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0], [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1], [0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0], [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1], [0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1], [0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0]]): |
1.-Sea un conjunto A y una relación R en A representada por la matriz M:
a) el conjunto A tiene 37 elementos
b) el conjunto A tiene 50 elementos
c) el conjunto A tiene 100 elementos
El cardinal de A es el número de filas (o de columnas) de M:
| > | rowdim(M); |
La respuesta correcta es la b).
b) simétrica pero no reflexiva
c) ni simétrica ni reflexiva
Traemos los procedimientos que necesitamos.
| > | Mref:=proc(M::matrix) local j,S,r: S:=0: for j from 1 to coldim(M) do S:=S+M[j,j]: od: if S=coldim(M) then r:="reflexiva": else r:="no reflexiva": fi: r; end: |
| > | Msim:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M-transpose(M)): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 then S:=1: fi: od: od: if S=1 then r:="no simetrica" else r:="simetrica" fi: r; end: |
| > | Mref(M); Msim(M); |
La respuesta correcta es la c).
b) ni antisimétrica ni transitiva
c) antisimetrica y no transitiva
Traemos los procedimientos que necesitamos.
| > | Mantisim:=proc(M::matrix) local S,i,j,r: S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if M[i,j]=1 and M[j,i]=1 and i<>j then S:=1: fi: od: od: if S=1 then r:="no antisimetrica" else r:="antisimetrica" fi: r; end: |
| > | Mtrans:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M^2): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 and M[i,j]=0 then S:=1: fi: od: od: if S=1 then r:="no transitiva" else r:="transitiva": fi:r; end: |
| > | Mantisim(M); Mtrans(M); |
La respuesta correcta es la b)
4.- La matriz de la clausura reflexiva de R tiene
a) 20 entradas distintas a las de M
b) 30 entradas distintas a las de M
c) 50 entradas distintas a las de M
Contamos el número de entradas nulas en la diagonal
| > | S:=0: for z from 1 to 50 do if M[z,z]=0 then S:=S+1: fi: od: S; |
La respuesta correcta es la c).
5.- La matriz de la clausura simétrica de la relación R tiene:
a) 2 entradas distintas a las de M
b) 3 entradas distintas a las de M
c) 5 entradas distintas a las de M
| > | Matrizdeunosyceros:=proc(M::matrix) local i,j,Mat; Mat:=matrix(rowdim(M),coldim(M),0); for i from 1 to rowdim(M) do for j from 1 to coldim(M) do if(M[i,j]<>0) then Mat[i,j]:=1; fi; od; od; RETURN(eval(Mat)); end: |
| > | N:=Matrizdeunosyceros(evalm(M+transpose(M))): |
Vamos a construir un procedimiento para contar el número de entradas diferentes entre dos matrices:
| > | Entradas:=proc(M::matrix, N::matrix) local S,z,t: S:=0: for z from 1 to coldim(M) do for t from 1 to coldim(M) do if N[z,t]<>M[z,t] then S:=S+1: fi: od: od: S; end: |
| > | Entradas(M,N); |
La respuesta correcta es la a).
6.- Sea el conjunto B y la relación S definidas abajo. Sea Ct la clausura transitiva de S:
a) Ct tiene 28 elementos más que S
b) Ct tiene 32 elementos más que S
c) Ct tiene 64 elementos más que S
| > | B:={1,2,3,4,5,6,7,8,9,0};
S:={[1,1],[1,2],[1,3],[2,2],[2,3],[2,5],[3,3],[3,5],[3,5],[3,6],[4,5],[4,6],[4,7],[5,5],[8,5],[8,6],[8,7],[8,8],[8,9],[9,5],[9,9],[9,6],[0,0],[0,1],[0,5],[8,0],[0,4],[4,0],[7,7],[7,8],[4,3],[4,4],[8,3],[0,1],[1,0]}; |
Calculamos la matriz de la relación:
| > | MatrizRelacion:=proc(D::list,R::set([anything,anything])) local i,j,L; L:=[]; for i from 1 to nops(D) do for j from 1 to nops(D) do if member([[op(D)][i],[op(D)][j]],R) then L:=[op(L),1] else L:=[op(L),0]; fi; od; od; evalm(matrix(nops(D),nops(D),L)); end: |
| > | A:=MatrizRelacion([1,2,3,4,5,6,7,8,9,0],S); |
| > | Warshall:=proc(M::matrix) local i,j,k,W,n; W:=matrix(rowdim(M),coldim(M),[seq(seq(M[i,j],j=1...coldim(M)),i=1..coldim(M))]): n:=coldim(M); for k from 1 to n do for i from 1 to n do for j from 1 to n do W[i,j]:=W[i,j]+(W[i,k]*W[k,j]); od; od; od; Matrizdeunosyceros(W); end: |
| > | L:=Warshall(A); |
| > | Entradas(A,L); |
La respuesta correcta es la a).
Si lo hacemos mediante el otro algoritmo:
| > | J:=Matrizdeunosyceros(evalm(add(A**i,i=1..10))): Entradas(A,J); |
a) es antisimétrica y transitiva
c) no es reflexiva ni simétrica ni transitiva
| > | Msim(A); Mref(A); Mantisim(A); Mtrans(A); |
| > |
La respuesta correcta es la c).
| > | P:=matrix(5,5,[1,1,1,1,a,1,1,1,b,1,a,1,1,1,1,0,0,0,0,0,a,a,a,b,1]); |
a) No hay ningún valor de a y b que la haga reflexiva
b) cualquier valor de a y b la hacen reflexiva
| > | P[4,4]; |
La respuesta correcta es la a).
9. Idem que 8 pero para la propiedad simétrica.
a) No hay ningún valor de a y b que la haga reflexiva
b) cualquier valor de a y b la hacen reflexiva
| > | evalm(P-transpose(P)); |
tiene entradas no nulas la matriz nunca puede ser simétrica, la respuesta correcta es la a).
10. Idem que 8 pero para la propiedad transitiva.
a) No hay ningún valor de a y b que la haga reflexiva
b) cualquier valor de a y b la hacen reflexiva
| > | evalm(Matrizdeunosyceros(evalm(P^2))-P); |
| > | Q:=matrix(5,5,[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,1,1,1,1,1]); |
| > | evalm(Q^2); |
| > |
| > | restart: with(linalg): |
Warning, the protected names norm and trace have been redefined and unprotected
| > | M:=matrix([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]): |
| > |
1.-Sea un conjunto A y una relación R en A representada por la matriz M:
a) el conjunto A tiene 84 elementos
b) el conjunto A tiene 50 elementos
c) el conjunto A tiene 45 elementos
El cardinal de A es el número de filas (o de columnas) de M:
| > | rowdim(M); |
La respuesta correcta es la c).
| > |
b) simétrica pero no reflexiva
c) ni simétrica ni reflexiva
Traemos los procedimientos que necesitamos.
| > | Mref:=proc(M::matrix) local j,S,r: S:=0: for j from 1 to coldim(M) do S:=S+M[j,j]: od: if S=coldim(M) then r:="reflexiva": else r:="no reflexiva": fi: r; end: |
| > | Msim:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M-transpose(M)): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 then S:=1: fi: od: od: if S=1 then r:="no simetrica" else r:="simetrica" fi: r; end: |
| > | Mref(M); Msim(M); |
La respuesta correcta es la b).
| > |
b) ni antisimétrica, ni transitiva
c) antisimétrica y no transitiva
Traemos los procedimientos que necesitamos.
| > | Mantisim:=proc(M::matrix) local S,i,j,r: S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if M[i,j]=1 and M[j,i]=1 and i<>j then S:=1: fi: od: od: if S=1 then r:="no antisimetrica" else r:="antisimetrica" fi: r; end: |
| > | Mtrans:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M^2): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 and M[i,j]=0 then S:=1: fi: od: od: if S=1 then r:="no transitiva" else r:="transitiva": fi:r; end: |
| > | Mantisim(M); Mtrans(M); |
La respuesta correcta es la b).
| > |
4.- La matriz de la clausura reflexiva de R tiene
a) 0 entradas distintas a las de M
b) 45 entradas distintas a las de M
c) 40 entradas distintas a las de M
Contamos el número de entradas nulas en la diagonal
| > | S:=0: for z from 1 to rowdim(M) do if M[z,z]=0 then S:=S+1: fi: od: S; |
La respuesta correcta es la b).
| > |
5.- La matriz de la clausura simétrica de la relación R tiene:
a) 0 entradas distintas a las de M
b) 10 entradas distintas a las de M
c) 4 entradas distintas a las de M
| > |
| > | Matrizdeunosyceros:=proc(M::matrix) local i,j,Mat; Mat:=matrix(rowdim(M),coldim(M),0); for i from 1 to rowdim(M) do for j from 1 to coldim(M) do if(M[i,j]<>0) then Mat[i,j]:=1; fi; od; od; RETURN(eval(Mat)); end: |
| > | N:=Matrizdeunosyceros(evalm(M+transpose(M))): |
| > |
| > | Entradas:=proc(M::matrix, N::matrix) local S,z,t: S:=0: for z from 1 to rowdim(M) do for t from 1 to coldim(M) do if N[z,t]<>M[z,t] then S:=S+1: fi: od: od: S; end: |
| > | Entradas(M,N); |
| > | iszero(evalm(M-N)); |
La respuesta correcta es la a).
| > |
6.- Sea el conjunto B y la relación S definidas abajo.
| > | B:={1,2,3,4,5,6,7,8,9,0}: S:={[1,1],[1,2],[1,3],[2,2],[2,3],[2,5],[3,3],[3,5],[3,5],[3,6],[4,5],[4,6],[4,7],[5,5],[8,5],[8,6],[8,7],[8,8],[8,9],[9,5],[9,9],[9,6],[0,0],[0,1],[0,5],[8,0],[0,4],[4,0],[7,7],[7,8],[4,3],[4,4],[8,3],[0,1],[1,0],[6,6]}: |
Sea Ct la clausura transitiva de S. Se verifica que:
b) Ct es una relación de orden total
c) Ct no es una relación de orden
| > | B:={1,2,3,4,5,6,7,8,9,0};
S:={[1,1],[1,2],[1,3],[2,2],[2,3],[2,5],[3,3],[3,5],[3,5],[3,6],[4,5],[4,6],[4,7],[5,5],[8,5],[8,6],[8,7],[8,8],[8,9],[9,5],[9,9],[9,6],[0,0],[0,1],[0,5],[8,0],[0,4],[4,0],[7,7],[7,8],[4,3],[4,4],[8,3],[0,1],[1,0],[6,6]}; |
| > |
| > | MatrizRelacion:=proc(D::list,R::set([anything,anything])) local i,j,L; L:=[]; for i from 1 to nops(D) do for j from 1 to nops(D) do if member([[op(D)][i],[op(D)][j]],R) then L:=[op(L),1] else L:=[op(L),0]; fi; od; od; evalm(matrix(nops(D),nops(D),L)); end: |
| > | A:=MatrizRelacion([1,2,3,4,5,6,7,8,9,0],S); |
Se trata entonces de calcular la clausura transitiva. Lo hacemos mediante el algoritmo de Warshall:
| > | Warshall:=proc(M::matrix) local i,j,k,W,n; W:=matrix(rowdim(M),coldim(M),[seq(seq(M[i,j],j=1...coldim(M)),i=1..coldim(M))]): n:=coldim(M); for k from 1 to n do for i from 1 to n do for j from 1 to n do W[i,j]:=W[i,j]+(W[i,k]*W[k,j]); od; od; od; Matrizdeunosyceros(W); end: |
| > | L:=Warshall(A); |
| > | Mref(L); |
| > | Mantisim(L); |
La respuesta correcta es la c).
| > |
| > | P:=matrix(5,5,[[1,1,a*b,a*b,a],[1,1,1,1,a^3],[a,1,1,a*b,a],[a*b,1,a*b,a,b],[a^2,a*b,a*b,b,1]]): |
a) no hay valores de a y b que la hagan reflexiva
b) es reflexiva para cualquier valor de a y b
c) hay valores de a y b que la hagan reflexiva
| > | P:=matrix(5,5,[[1,1,a*b,a*b,a],[1,1,1,1,a^3],[a,1,1,a*b,a],[a*b,1,a*b,a,b],[a^2,a*b,a*b,b,1]]); |
La respuesta correcta es la c).
| > |
8.- Idem que 7 pero para la propiedad simétrica:
a) no hay valores de a y b que la hagan simétrica
b) es simétrica para cualquier valor de a y b
c) existen valores de a y b que la hagan simétrica
| > | evalm(P-transpose(P)); |
tiene todas las entradas nulas si
![]() = 0,
= 0,
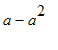 = 0 y
= 0 y
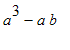 = 0, los posibles valores son
= 0, los posibles valores son
La respuesta correcta es la c).
| > |
a) no hay valores de a y b que la hagan de equivalencia
b) es de equivalencia para a=1 y b=0
c) es de equivalencia para a=1 y b=1
| > | a:=1;b:=1;P:=matrix(5,5,[[1,1,a*b,a*b,a],[1,1,1,1,a^3],[a,1,1,a*b,a],[a*b,1,a*b,a,b],[a^2,a*b,a*b,b,1]]); Mtrans(P); |
| > | Matrizdeunosyceros:=proc(M::matrix) local i,j,Mat; Mat:=matrix(rowdim(M),coldim(M),0); for i from 1 to rowdim(M) do for j from 1 to coldim(M) do if(M[i,j]<>0) then Mat[i,j]:=1; fi; od; od; RETURN(eval(Mat)); end: |
| > | evalm(Matrizdeunosyceros(evalm(P^2))-P); |
La respuesta correcta es la c).
| > |
| > |
| > | B:=matrix([[1, 0, 0, 0, 1, 0, 0, 0], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1], [1, 0, 0, 0, 1, 0, 0, 0], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1]]): |
| > |
| > | B:=matrix([[1, 0, 0, 0, 1, 0, 0, 0], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1], [1, 0, 0, 0, 1, 0, 0, 0], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1], [0, 1, 1, 1, 0, 1, 1, 1]]); |
| > | Mref:=proc(M::matrix) local j,S,r: S:=0: for j from 1 to coldim(M) do S:=S+M[j,j]: od: if S=coldim(M) then r:="reflexiva": else r:="no reflexiva": fi: r; end: |
| > | Mref(B); |
| > | Msim:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M-transpose(M)): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 then S:=1: fi: od: od: if S=1 then r:="no simetrica" else r:="simetrica" fi: r; end: |
| > | Msim(B); |
| > | Mtrans:=proc(M::matrix) local N,S,i,j,r: N:=evalm(M^2): S:=0: for i from 1 to rowdim(M) while S=0 do for j from 1 to rowdim(M) do if N[i,j]<>0 and M[i,j]=0 then S:=1: fi: od: od: if S=1 then r:="no transitiva" else r:="transitiva": fi:r; end: |
| > | Mtrans(B); |
| > |
La respuesta correcta es la a).
| > | #fin |
| > |