 |
Web Hosting by Netfirms | Free Domain Names by Netfirms |
|
 |
El principio de inducción matemática consiste en lo siguiente:
Una proposición es válida para todo número natural n si:
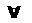k[p(k) --> p(k + 1)] --> 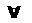np(n)En esa misma sección se estudió la demostración por contradicción. Demostrar una proposición de la forma p --> q, es equivalente a demostrar esta proposición de la forma [((p ^ ~q) --> (r ^ ~r)]. Es decir, la negación de la proposición p --> q, vimos que es equivalente a p ^ ~q, que es exactamente lo que consiste la demostración por contradicción, esta nos lleva a una expresión de la forma r ^ ~r, que es una falsedad, en virtud de esto, se concluye que la negación de la proposición p --> q es falsa.
Antes de ver la demostración del Principio de Inducción Matemática, quiero poner en claro lo siguiente:
El antecedente del principio de inducción, consta de dos partes:
1. La proposición es válida para n = 1
2. Si la proposición es válida para un número natural cualquiera n = k entonces es válida para el número n = k + 1.
El
consecuente del principio de inducción, nos dice que si lo anterior se
cumple, es decir si las dos partes del antecedente son válidas para una
proposición, entonces esta sigue siendo válida para todo número natural
n.
Ahora bien, la demostración por contradicción, consiste en la negación
del consecuente, y hacer válido el antecedente. Para la demostración
por contradicción del principio de inducción matemática negamos el
consecuente, es decir, la proposición no es válida para todo número
natural n, y se hacen válidas las dos partes del antecedente.
Una proposición es válida para todo número natural n si:
Demostración.
Supongamos lo contrario, es decir, que la proposición no es válida para
cualquier número natural n. Entonces existe un número natural, digamos
m tal que:
1) Para n = m la proposición es falsa y:
2) Para todo n menor a m la proposición es verdadera.
En otras palabras, m es el primer número natural para el cual resulta falsa la proposición.
Es evidente que m > 1 pues para n = 1 la proposición es verdadera
(por la condición 1 primera parte del antecedente del teorema). Además
m - 1 es un número natural, ya que m es natural. Pero entonces la
proposición es válida para el número natural m - 1 y no lo es para el
número natural siguiente m. Esto contradice la condición 2 (segunda
parte del antecedente del teorema).
Así se ha llegado a una contradicción r ^ ~r. Dicha contradicción
resultó al afirmar que la proposición es falsa para cualquier número
natural. Por tanto si se cumplen las condiciones iniciales: la
proposición es válida para n = 1 y si es válida para el número n = k
entonces es válida para el siguiente número n = k + 1, entonces, la
proposición es válida para todo número natural n.
Toda demostración que
se basa en el principio de inducción matemática se denomina
demostración por inducción (por el método de inducción matemática). Tal
demostración consta de dos partes, es decir, verificar que se cumplan
las dos condiciones:
La proposición es válida para n = 1
La proposición es válida para n = k + 1 si lo es para n = k, donde k es un número arbitrario.
Si estas condiciones se cumplen, podemos afirmar, en virtud del
principio de inducción matemática, que la proposición es válida para
todo número natural.
Antes de pasar a la demostración de identidades de problemas
aritméticos, lo mejor es ver un ejemplo de como se utiliza el principio
de inducción matemática en algunos ejemplos, así como de hacer varias
observaciones del mismo principio.
Consideremos de nueva cuenta la suma:
Sabemos ya que de la sección anterior que:
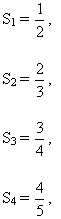
Ahora bien, no
repetiremos el mismo error cometido en la sección anterior de "afirmar"
de inmediato que para todo número natural n es
1) Para n = 1 la fórmula se cumple pues:
Resaltan a la vista las siguientes observaciones:
Observacion 1.
Es necesario subrayar que la demostración por inducción exige
incondicionalemente la demostración de las dos partes del principio de
inducción.
Hemos visto a que conduce despreciar la parte 2) de este principio (ejemplo 2, de la seccion anterior).
Ahora se mostrará que tampoco se puede omitir la parte 1). Veamos el siguiente ejemplo:
Todo número natural es igual al número natural siguiente.
Apliquemos para la demostración el método de inducción matemática. Supongamos que:
Corolario. ¡¡Todos los números naturales son iguales!!.
¿ Dónde radica el error ?
El error consiste en que la primera parte del principio de inducción
matemática, no ha sido demostrada (ni puede ser demostrada) y sólo ha
sido demostrada la segunda parte.
Cada una de las partes 1) y 2) desempeña su papel.
La parte 1) crea, la base de inducción. La parte 2) permite ampliar
automática e indefinidamente esta base pasando de un caso particular al
siguiente, es decir, de n a n + 1.
Si no ha sido demostrada la parte 1) pero ha sido demostrada la
parte 2) (ejemplo anterior), no se ha creado la base de inducción y no
tiene sentido aplicar la parte 2), pues no hay nada que ampliar.
Si no ha sido demostrada la parte 2), pero ha sido demostrada la parte
1) (ejemplos 1 y 2 de la sección anterior), existe la base de inducción
pero no tenemos el derecho de ampliarla.
Observación 2.
Hemos explicado el método de inducción matemática en el caso más
sencillo. En situaciones más complejas habrá que modificar
respectivamente los enunciados de las partes 1) y 2) de la inducción.
A veces la segunda parte
de la demostración se basa en que la proposición es válida no sólo para
n = k sino también para n = k - 1. En tal caso la proposición de la
primera parte debe comprobarse para dos valores sucesivos de n.
A veces, en la segunda parte se demuestra la proposición para un valor de n suponiéndose su validez para todos los número naturales k menores que n.
A veces la proposición se demuestra para
todo número entero n mayor que un número entero m (y no para cualquier
número natural). En este caso la primera parte debe consistir en
demostrar la proposición para n = m + 1 y, si es necesario, para
algunos valores de n.
Mas adelante se verán este tipo de ejemplos.
Para llegar a dominar la demostración por el método de inducción
matemática, es necesario la práctica, realizando para esto muchos
ejercicios.
De aquí en adelante se verán muchos ejercicios para que puedas
adentrarte al mundo de la demostración usando el método de inducción
matemática.