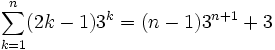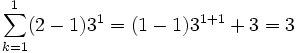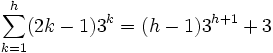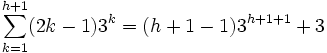La elección de stewards de la Fundación Wikimedia 2009 ha empezado. Por favor, vota.
[Contraer]
[Ayúdanos traduciendo.] 

Inducción matemática

De Wikipedia, la enciclopedia libre

La inducción es un razonamiento que permite demostrar una infinidad de proposiciones, o una proposición que depende de un parámetro n que toma una infinidad de valores enteros. En términos simples, la inducción matemática consiste en el siguiente razonamiento:

Premisa mayor El número entero a tiene la propiedad P
Premisa menor El hecho de que cualquier número entero n tenga la propiedad P implica que n + 1 también la tiene
Conclusión Todos los números enteros a partir de a tienen la propiedad P

Demostraciones por inducción [editar]

El razonamiento para demostrar una proposición cualquiera mediante el esquema del razonamiento es el siguiente: Llamemos Pn la proposición al rango n.

  • Se demuestra que P0 es cierta (iniciación de la inducción).
  • Se demuestra que si se asume Pn como cierta, entonces Pn+1 lo es también, y esto sin condición sobre el entero natural n. (relación de inducción).

Luego, demostrado esto, concluímos por inducción, que Pn es cierto para todo natural n.

La inducción puede empezar por otro término que P0, digamos por Pno. Entonces Pn será válido a partir del rango no, es decir, para todo natural n ≥ no.

Ejemplo: Demostremos que para todo n ≥ 1, 6n es un número que acaba en 6.

Sea Pn la proposición: "6n acaba en 6".
  • Es claro que P1 es cierto, porque 61 = 6.
  • Supongamos que Pn es cierto para un valor de n natural, y probemos Pn+1.
Un entero acaba por 6 si se puede escribir así: 10a + 6, con a entero positivo o igual a cero. La hipótesis es, pues, 6n = 10a + 6.
Entonces 6n+1 = 6(10a + 6) = 60a + 36 = 60a + 30 + 6 = 10(6a + 3) + 6 = 10c + 6, con c=6a + 3, entero.
Esta última escritura prueba que 6n+1 acaba por 6, o sea que Pn+1 es cierto.
Luego Pn es cierto para todo n ≥ 1.

La inducción es válida por la construcción misma del conjunto de los naturales mediante los axiomas de Peano. De hecho, la inducción imita la construcción del conjunto: 0 es un natural, y, si n lo es, entonces n+1 (sucesor de n) lo es también.
Existen otras inducciones, para otros conjuntos elaborados de forma distinta, como por ejemplo la inducción transfinita, y la inducción sobre las fórmulas de la lógica proposicional.

Además de la Demostración por Inducción, existe la definición o construcción por inducción. Por ejemplo, una sucesión aritmética puede ser definida como función de n: un = a + rn, o por inducción:

  • u0 = a
  • un+1 = un + r.

(véase también la Definición de Pitatoria por Inducción)

Otro ejemplo [editar]

Se analiza la siguiente proposición
\sum_{k=1}^n (2k - 1) 3^k = (n - 1) 3^{n+1} + 3 \forall n \in \mathbb{N}
Se analiza si es verdadera para n=1
\sum_{k=1}^1 (2 - 1) 3^1 = (1 - 1) 3^{1+1} + 3 = 3

Por lo tanto la proposición es verdadera para n=1

Hipótesis inductiva
\sum_{k=1}^h (2k - 1) 3^k = (h - 1) 3^{h+1} + 3
Tesis inductiva
\sum_{k=1}^{h+1} (2k - 1) 3^k = (h + 1 - 1) 3^{h+1+1} + 3
\sum_{k=1}^{h+1} (2k - 1) 3^k = h 3^{h+2} + 3
Demostración
\sum_{k=1}^{h+1} (2k - 1) 3^k = (h - 1) 3^{h+1} + 3 + [2(h+1) - 1] 3^{h+1}
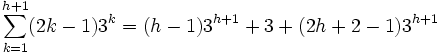
\sum_{k=1}^{h+1} (2k - 1) 3^k = (h - 1) 3^{h+1} + 3 + (2h+2 - 1) 3^{h+1}
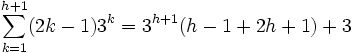\sum_{k=1}^{h+1} (2k - 1) 3^k = 3^{h+1} (h - 1 + 2h + 1) + 3 (sacando factor común)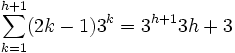
\sum_{k=1}^{h+1} (2k - 1) 3^k = 3^{h+1} 3h + 3
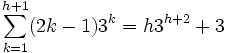
\sum_{k=1}^{h+1} (2k - 1) 3^k = h 3^{h+2} + 3

Por lo tanto la proposición es verdadera 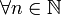\forall n \in \mathbb {N}

Véase también [editar]

Obtenido de "http://es.wikipedia.org/wiki/Inducci%C3%B3n_matem%C3%A1tica"
Herramientas personales