Circuitos digitales: Álgebra de Boole

1. ÁLGEBRA DE BOOLE.

    El álgebra de Boole se llama así debido a George Boole, quien la desarrolló a mediados del siglo XIX. El álgebra de Boole denominada también álgebra de la lógica, permite prescindir de la intuición y simplificar deductivamente afirmaciones lógicas que son todavía más complejos.

    El objetivo principal de este tema es llegar a manejar los postulados y teoremas del álgebra de Boole como herramienta básica en el análisis y síntesis de circuitos digitales.

    Si lo desea, elija alguna opción haciendo clic sobre ella.

1.1 DEFINICIONES

1. Se establecen los conceptos fundamentales (símbolos o términos no definidos).

2. Se define un conjunto de postulados que forman la base del álgebra.

3. Se constituyen los teoremas fundamentales del álgebra a partir de los postulados.

    A su vez, las exigencias y condiciones que deben reunir los postulados son:

1. Los postulados deben ser coherentes o consistentes para que una álgebra definida pueda desarrollarse por deducciones lógicas. En caso contrario, el sistema resulta contradictorio.

2. Los postulados deben ser independientes; es decir irreductibles recíprocamente (libre de reducciones)

3. Los postulados deben ser tan simples en su enunciado como sea posible; es decir, no separables en dos o más partes.

1.2 POSTULADOS.

P.1. Existe un conjunto M de elementos sujetos a una relación de equivalencia denotada por el signo = que satisfacen el principio se sustitución.

P.2.a. Para toda (A, B) en M, A + B es una operación binaria (suma lógica) denotada por el signo +, tal que:

(A + B) está en M

Es decir, el conjunto M es cerrado a esta operación.

P.2.b. Para toda (A, B) en M, A . B es una operación binaria (producto lógico) denotada por el signo ., tal que:

(A . B) está en M

Es decir, el conjunto M es cerrado a esta operación.

P.3.a. Existe un elemento 0 en M, tal que:

A + 0 = A

para toda A en M.

P.3.b. Existe un elemento 1 en M, tal que:

A . 1 = A

para toda A en M.

P.4.a. Para toda (A, B) en M:

A + B = B + A

Se satisface la propiedad conmutativa

P.4.b. Para toda (A, B) en M:

A . B = B . A

Se satisface la propiedad conmutativa

P.5.a. Para toda (A, B, C) en M:

A + (B . C) = (A + B) . (A + C)

Ley distributiva de la suma sobre el producto

P.5.b. Para toda (A, B, C) en M:

A . (B + C) = (A . B) + (A . C)

Ley distributiva del producto sobre la suma

P.6.a. Para todo elemento A en M, existe un elemento A', tal que:

A + A' = 1

P.6.b. Para todo elemento A en M, existe un elemento A', tal que:

A . A' = 0

P.7. Existen por lo menos (A, B) en M, tal que:

A es diferente de B

    Se habrá observado cierta similitud entre estos postulados y los del álgebra ordinaria. Nótese sin embargo, que la primera ley distributiva P.5.a. no es válida en el álgebra ordinaria y que tampoco existe ningún elemento A' en dicha álgebra.

    También se notará que los postulados se presentaron por pares. Una observación más detenida, muestra que existe una dualidad entre los símbolos + y ., lo mismo que entre los dígitos 1 y 0. Si el símbolo + se sustituye por . y . por +, así como todos los UNOS se sustituyen por CEROS y los CEROS por UNOS, en cualquiera de los postulados de cada par, el resultado es el otro postulado. A causa de esta dualidad fundamental, cada teorema que se presenta tendrá su dual que se obtendrá efectuando la sustitución mencionada; por tanto, la demostración de un teorema implica la validez de su teorema dual.

1.3 TEOREMAS FUNDAMENTALES.

    A continuación se presentan los teoremas principales del álgebra de Boole, los cuales son la base del trabajo subsecuente. Es posible demostrar dichos teoremas por cualesquiera de los siguientes métodos:

1. Algebraicamente (empleando postulados y teoremas ya demostrados).

2. Gráficamente (por medio de los diagramas de Venn).

3. Por inducción perfecta (empleando tablas de verdad).

    Aquí se empleará el método algebraico pues se considera la mejor manera de iniciarse en esta álgebra, además de que sólo se demostrarán los teoremas primales, pero aplicando las reglas de dualidad mencionadas anteriormente, se podrá obtener la parte dual.

T.1. Teoremas sobre la UNICIDAD.

1.a. El elemento 0 es único.

1.b. El elemento 1 es único.

Demostración de 1.a.

Por contradicción, supóngase que 0 y 01 son neutros aditivos, por lo que deben satisfacer al postulado P.3.a, es decir:

A + 0 = A   y   A1 + 01 = A1

Si A1 = 0 y A = 01 y como 0 es neutro, por suposición, entonces:

01 + 0 = 0                (1)

Además como 01 es neutro, por suposición, entonces:

0 + 01 = 0                     (2)

De (1) y (2) se tiene:

01 = 0

con lo que se demuestra el teorema.

T.2. Teoremas sobre la EQUIPOTENCIA.

2.a. A + A = A

2.b. A . A = A

Demostración de 2.a.

A + A = (A + A) . 1               (P.3.b.)

A + A = (A + A) . (A + A')        (P.6.a.)

A + A = A + (A . A')              (P.5.a)

A + A = A + 0                    (P.6.b.)

A + A = A                                (P.3.a.)

T.3.

3.a. A + 1 = 1

3.b. A . 0 = 0

Demostración de 3.a.

A + 1 = 1 . (A + 1)                (P.3.b.)

A + 1 = (A + A') . (A + 1)    (P.6.a)

A + 1 = A + (A' . 1)            (P.5.a)

A + 1 = A + A'                    (P.3.b.)

A + 1 = 1                             (P.6.a.)

T.4. Teoremas de ABSORCIÓN.

4.a. A + (A . B) = A

4.b. A . (A + B) = A

Demostración de 4.a.

A + (A . B) = (A . 1) + (A . B)         (P.3.b.)

A + (A . B) = A . (1 + B)                (P.5.b.)

A + (A . B) = A . 1                        (T.3.a.)

A + (A . B) = A                             (P.3.b.)

T.5. El elemento A' es único.

Demostración

Por contradicción, supóngase que existen dos elementos distintos A'1 y A'2, tales que satisfacen los postulados P.6.a. y P.6.b., es decir:

  A + A'1 = 1   y   A + A'2 = 1
A . A'1 = 0   y   A . A'2   = 0

Entonces:

A'2 = 1 . A'2                                 (P.3.b)

A'2 = (A + A'1) . A'2                     (por suposición)

A'2 = (A . A'2 ) + (A'1 . A'2)         (P.5.b.)

A'2 = 0 + (A'1 . A'2)                    (por suposición)

A'2 = (A . A'1) + (A'1 . A'2)         (por suposición)

A'2 = (A + A'2) . A'1                     (P.5.b)

A'2 = 1 . A'1                                 (por suposición)

A'2 = A'1                                     (P.3.b.)

T.6. Para toda A en M, A = A''

Demostración

Sea A'' = X, por tanto:

A' + X = 1   y   A' , X = 0             (P.6.)

Pero:

A' + A = 1   y   A' . A = 0                 (P.6.)

Así que tanto X como A' satisfacen el postulado P.6. como el complemento de A, por tanto:

X = A, es decir, A'' = A

T.7. Teoremas de ABSORCIÓN

7.a. A . [(A + B) + C] = [(A + B) + C] . A = A

7.b. A + [(A . B) . C] = [(A . B) . C] = A

Demostración de 7.a.

A . [(A + B) + C] = A . (A + B) + (A . C)                     (P.5.b.)

A . [(A + B) + C] = (A . A) + (A . B) + (A . C)             (P.5.b.)

A . [(A + B) + C] = A + (A . B) + (A . C)                     (T.2.)

A . [(A + B) + C] = A . (1 + B + C)                            (P.5.b.)

A . [(A + B) + C] = A . 1                                               (T.3.)

A . [(A + B) + C] = A                                                    (P.3.b.)

T.8. Teoremas sobre la ASOCIACIÓN.

8.a. A + (B + C) = (A + B) + C

8.b. A . (B . C) = (A . B) . C

Demostración de 8.a.

Sea:

Z = [(A + B) + C] . [A + (B + C)]

Z = {A . [(A + B) + C]} + {(B + C) . [(A + B) + C]}             (P.5.b.)

Z = A + {(B + C) . [(A + B) + C]}                                        (T.7.)

Z = A + {B . [(A + B) + C] + C . [(A + B) + C]}                  (P.5.b.)

Z = A + {B + C . [(A + B) + C]}                                          (T.7.)

Z = A + (B + C)                                                                     (T.7.)            (1)

Como:

Z = [(A + B) + C] . [A + (B + C)]

Z = {(A + B) . [A + (B + C)]} + {C . [A + (B + C)]}           (P.5.b.)

Z = {(A + B) . [A + (B + C)]} + C                                        (T.7.)

Z = {A . [A + (B + C)] + B . [A + (B + C)]} + C                 (P.5.b.)

Z = {A . [A + (B + C)] + B} + C                                         (T.7.)

Z = (A + B) + C                                                                  (T.7.)             (2)

Por consiguiente, de (1) y (2) y por transitividad:

Z = A + (B + C) = (A + B) + C = A + B + C

T.9. Teoremas sobre la COMPLEMENTACIÓN.

9.a. A + (A' . B) = A + B

9.b. A . (A' + B) = A . B

Demostración de 9.a.

A + (A' . B) = (A + A') . (A + B)             (P.5.a.)

A + (A' . B) = 1 . (A + B)                         (P.6.a.)

A + (A' . B) = A + B                               (P.3.b.)

T.10. Teoremas de DeMORGAN.

10. a. (A + B)'' = A' . B'

10.b. (A . B)' = A' + B'

Demostración de 10.a.

Primera parte:

(A + B) + (A' . B') = [(A + B) + A'] . [(A + B) + B']             (P.5.a.)

(A + B) + (A' . B') = [A' + (A + B)] . [(A + B) + B']             (P.4.a.)

(A + B) + (A' . B') = [(A' + A) + B] . [A + (B + B')]           (T.8.)

(A + B) + (A' . B') = (1 + B) . (A + 1)                                 (P.6.a.)

(A + B) + (A' . B') = 1 . 1                                                    (T.3.a.)

(A + B) + (A' . B') = 1                                                         (T.2.b.)                (1)

Segunda parte:

(A + B) . (A' . B') = (A' . B') . (A + B)                              (P.4.b.)

(A + B) . (A' . B') = (A' . B' . A) + (A' . B' . B)                (P.5.b.)

(A + B) . (A' . B') = 0 + 0                                                 (P.6.b.)

(A + B) . (A' . B') = 0                                                         (T.2.a.)                (2)

Por tanto, de (1) y (2) se concluye que:

(A + B)' = A' . B'

T.11.

11.a. (A . B) + (A' . C) + (B . C) = (A . B) + (A' . C)

11.b. (A + B) . (A' + C) . (B + C) = (A + B) . (A' + C)

Demostración de 11.a.

(A . B) + (A' . C) + (B . C) = (A . B . 1) + (A' . 1 . C) + (1 . B . C) =                     (P.3.b.)

= [A . B . (C + C')] + [A' . (B + B') . C] + [(A + A') . B . C ] =                    (P.6.b.)

= (A B C) + (A B C') + ( A' B C) + (A' B' C) + (A B C) + (A' B C) =        (P.5.b.)

= (A B C) + (A B C') + ( A' B C) + (A' B' C) =                                             (T.2.)

= [A . B . (C + C')] + [A' . C . (B + B')] =                                                      (P.5.a.)

= (A . B . 1) + (A' . C . 1)                                                                                (P.6.a.)

(A . B) + (A' . C) + (B . C) = (A . B) + (A' . C)                                                        (P.3.b.)

T.12.

12.a. (A . B) + (A . B' . C) = (A . B) + (A . C)

12.b. (A + B) . (A + B' + C) = (A + B) . (A + C)

Demostración de 12.a.

(A . B) + (A . B' . C) = A . [B + (B' . C)]                                             (P.5.b.)

(A . B) + (A . B' . C) = A . [(B + B') . (B + C)] = A . (B + C)            (T.9.a.)

(A . B) + (A . B' . C) = (A . B) + (A . C)                                              (P.5.b.)

T.13.

13.a. (A . B) + (A . B') = A

13.b. (A + B) . (A + B') = A

Demostración de 13.a.

(A . B) + (A . B') = A . (B + B')              (P.5.b.)

(A . B) + (A . B') = A . 1                         (P.6.b.)

(A . B) + (A . B') = A

Para fácil referencia, los teoremas se resumen en la siguiente tabla:

1.4 COMPUERTAS LÓGICAS

Un computador digital, como su nombre lo indica, es un sistema digital que realiza diversas operaciones de cómputo. La palabra Digital implica que la información que se representa en el computador por medio de variables que toman un número limitado de valoresViscretos o cuantizados. Estos valores son procesados íntemamente por componentes que pueden mantener un número limitado de estados discretos. Los dígitos decimales por ejemplo, proporcionan 10 valores discretos ( 0 .. 9 ). Como sabemos en la práctica, los computadores funcionan más confiablemente si sólo utilizan dos estados equiprobables. Debido al hecho que los componentes electrónicos atienden a dos estados ( encendido / apagado ) y que la lógica humana tiende a ser binaria ( esto es, cierto o falsa, si o no ) se utiliza el sistema binario y se dice que son binarias.

Los computadores digitales utilizan el sistema de números binarios, que tiene dos dígitos 0 y 1. Un dígito binario se denomina un bit. ' La infonnación está representada en los computadores digitales en grupos de bits. Utilizando diversas técnicas de codificación los grupos de bits pueden hacerse que representen no solamente números binarios sino también otros símbolos discretos cualesquiera, tales como dígitos decimales o letras de alfabeto. Utilizando arreglos binarios y diversas técnicas de codificación, los dígitos binarios o grupos de bits pueden utilizarse para desarrollar conjuntos completos de instrucciones para realizar diversos tipos de cálculos.

La información binaria se representa en un sistema digital por cantidades físicas denominadas señales, Las señales eléctricas tales como voltajes existen a través del sistema digital en cualquiera de dos valores reconocibles y representan un a variable binaria igual a 1 o 0. Por ejemplo, un sistema digital particular puede emplear una señal de 3 [volts 1 para representar el binario "I" y 0.5 [volts 1 para el binario "0". La siguiente ilustración muestra un ejemplo de una señal binaria.

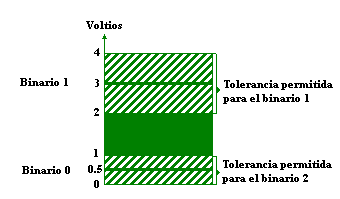
Como se muestra en la figura, cada valor binario tiene una desviación aceptable del valor nominal. La región íntermedia entre las dos regiones permitidas se cruza solamente durante la transición de estado.  Los terminales de entrada de un circuito digital aceptan señales binarias dentro de las tolerancias permitidas y los circuitos responden en los terminales de salida con señales binarias que caen dentro de las tolerancias permitidas.

La lógica binaria tiene que ver con variables binarias y con operaciones que toman un sentido lógico. Es utilizada para escribir, en forma algebraica o tabular. La manipulación y. procesamiento de información binaria. La manipulación de información binaria se hace por circuitos lógico que se denominan Compuertas.

Las compuertas son bloques del hardware que producen señales del binario 1 ó 0 cuando se satisfacen los requisitos de entrada lógica. Las diversas compuertas lógicas se encuentran comúnmente en sistemas de computadores digitales. Cada compuerta tiene un símbolo gráfico diferente y su operación puede describirse por medio de una función algebraica. Las relaciones entrada - salida de las variables binarias para cada compuerta pueden representarse en forma tabular en una tabla de verdad.

A continuación se detallan los nombres, símbolos, gráficos, funciones algebraicas, y tablas de verdad de ocho compuertas.

Compuerta AND: 

Cada compuerta tiene una o dos variables de entrada designadas por A y B y una salida binaria designada por x. La compuerta AND produce la unión lógica AND: esto es: la salida es 1 si la entrada A y la entrada B están ambas en el binario 1: de otra manera, la salida es 0. Estas condiciones también son especificadas en la tabla de verdad para la compuerta AND. La tabla muestra que la salida x es 1 solamente cuando ambas entradas A y B están en 1 . El símbolo de operación algebraico de la función AND es el mismo que el símbolo de la multiplicación de la aritmética ordinaria (*). Podemos utilizar o un punto entre las variables o concatenar las variables sin ningún símbolo de operación entre ellas. Las compuertas AND pueden tener más de dos entradas y por definición, la salida es 1 si cualquier entrada es 1.

Compuerta OR: 

La compuerta OR produce la función OR inclusiva, esto es, la salida es 1 si la entrada A o la entrada B o ambas entradas son 1; de otra manera, la salida es 0. El símbolo algebraico de la función OR (+), similar a la operación de aritmética de suma. Las compuertas OR pueden tener más de dos entradas y por definición la salida es 1 si cualquier entrada es 1.

Compuerta NOT (Inversor):

El circuito inversor invierte el sentido lógico de una señal binaria. Produce el NOT,. o función complemento. El símbolo algebraico utilizado para el complemento es una barra sobra el símbolo de la variable binaria. Si la variable binaria posee un valor 0, la compuerta NOT cambia su estado al valor 1 y viceversa. El círculo pequeño en la salida de un símbolo gráfico de un inversor designa un complemento lógico. Es decir cambia los valores binarios 1 a 0 y viceversa.

Compuerta Separador:

Un símbolo triángulo por sí mismo designa un circuito separador no produce ninguna función lógica particular puesto que el valor binario de la salida es el mismo de la entrada. Este circuito se utiliza simplemente para amplificación de la señal. Por ejemplo, un separador que utiliza i volt para el binario 1 producirá una salida de 3 volt cuando la entrada es 3 volt. Sin embargo, la corriente suministrada en la entrada es mucho más pequeña que la corriente producida en la salida. De ésta manera, un separador puede excitar muchas otras compuertas que requieren una cantidad mayor de corriente que de otra manera no se encontraría en la pequeña cantidad de corriente aplicada a la entrada del separador.

Compuerta NAND:

Es el complemento de la función AND, como se indica por el símbolo gráfico que consiste en un símbolo gráfico AND seguido por un pequeño círculo. La designación NAND se deriva de la abreviación NOT - AND. Una designación más adecuada habría sido AND invertido puesto que Es la función AND la que se ha invertido.

Compuerta NOR:  

La compuerta NOR es el complemento de la compuerta OR y utiliza un símbolo gráfico OR seguido de un círculo pequeño. Tanto las compuertas NAND como la NOR pueden tener más de dos entradas, y la salida es siempre el complemento de las funciones AND u OR, respectivamente.

Compuerta OR exclusivo (XOR):

La compuerta OR exclusiva tiene un símbolo gráfico similar a la compuerta OR excepto por una línea adicional curva en el lado de la entrada. La salida de esta compuerta es 1 si cada entrada es 1 pero excluye la combinación cuando las dos entradas son 1. La función OR exclusivo tiene su propio símbolo gráfico o puede expresarse en términos de operaciones complementarias AND, OR .

Compuerta NOR exclusivo (XOR):

El NOR exclusivo como se indica por el círculo pequeño en el símbolo gráfico. La salida de ésta compuerta es 1 solamente si ambas entradas son tienen el mismo valor binario. Nosotros nos referiremos a la función NOR exclusivo como la función de equivalencia. Puesto que las funciones OR exclusivo y funciones de equivalencia no son siempre el complemento la una de la otra. Un nombre más adecuado para la operación OR exclusivo sería la de una función impar; esto es, la salida es 1 si un número impar de entrada es 1. Así en una función OR (impar) exclusiva de tres entradas, la salida es 1 si solamente la entrada es 1 o si todas las entradas son 1. La función de equivalencia es una función par; esto es, su salida es 1 si un número par de entradas es 0. Para un función de equivalencia de tres entradas, la salida es 1 si ninauna de las entradas son 0 ( todas las entradas son 1 ) o si dos de las entradas son 0 ( una entrada es 1 Una investigación cuidadosa revelará que el OR exclusivo y las funciones de equivalencia son el complemento la una de la otra cuando las compuertas tienen un número par de entradas, pero las dos funciones son iguales cuando el número de entradas es impar. Estas dos compuertas están comúnmente disponibles con dos entradas y solamente en forma rara se encuentran con tres o más entradas. 

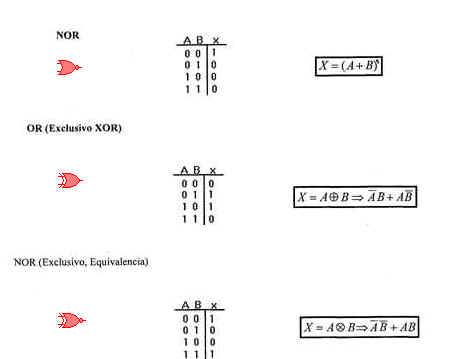
Retornemos el teorema De Morgan:

El teorema De Morgan es muy importante al tratar compuertas NOR y NAND. Expresa que una compuerta NOR que realiza la función (x + y)' es equivalente a la expresión función xy' . Similarmente, una función NAND puede ser expresada bien sea por (xy)' o por x' + y' por esta razón, las compuertas NOR y NAND tienen dos símbolos gráficos distintos como se muestra en la figura:

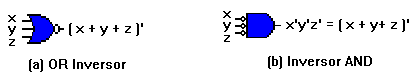
En vez de representar una cornpuerta NOR por el símbolo gráfico OR seguido por un círculo, nosotros podemos representarla por un símbolo gráfico AND precedido por círculos en todas las entrada. El inversor AND para la compuerta NOR proviene M teorema De Morgan y de la convención de que los círculos pequeños denotan complementación. Similarmente la compuertaNAND también posee dos símbolos gráficos.

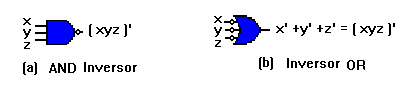
Para ver cómo se utiliza la manipulación del álgebra Booleana para simplificar circuitos digitales considere el diagrama lógico de la siguiente figura. La salida de la primera compuerta NAND es, por el teorema De Morgan, (AB)' = A' + B'  . La salida del circuito es la operación NAND de este término y B' .

X = [( A' + B ) * B' ] '

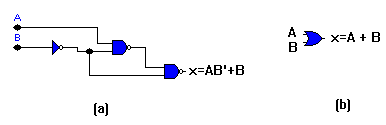
Utilizando el teorema De Morgan dos veces, obtenemos:

X = (A' + B)' + B = AB' + B

Note que el teorema De Morgan ha sido aplicado tres veces   ( para demostrar su utilización ) pero podría ser aplicado solamente una vez de la siguiente manera:

X = [ ( AB' )*B']' = AB' + B

La expresión para x puede simplificarse por aplicación de las relaciones mencionadas anteriormente

X  = AB'+ B

    = B + AB'

    = ( B + A) ( B + B')

    = (B+A)* 1

    = B + A

    = A + B

El resultado final produce una función OR y puede ser implementado con una sola compuerta OR como se muestra en la figura parte (b). Uno Puede demostrar que dos circuitos producen relaciones binarias idénticas Entrada - Salida simplemente obteniendo la tabla de verdad para cada uno de ellos.